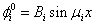 (16) (16)
 (17) (17)
 (18) (18)
式中,常数Bi由初始条件确定。
一阶摄动 需满足简支梁的边界条件式(7),式(13)的解可以表示成 需满足简支梁的边界条件式(7),式(13)的解可以表示成 (j=1,2,3,···)的线性组合 (j=1,2,3,···)的线性组合
 (19) (19)
式中, 为线性组合系数。 为线性组合系数。
将式(17)、(10)和(11)代入式(9),得
 (20) (20)
根据式(12),式(19)可进一步简化成
 (21) (21)
为了求得n2个 和n个 和n个 的值,将式(21)乘以第k阶完整梁的模态振型 的值,将式(21)乘以第k阶完整梁的模态振型 ,并在整个梁长度上进行积分,考虑到模态的正交性 ,并在整个梁长度上进行积分,考虑到模态的正交性 ,则有 ,则有
  (22) (22)
根据 ,可得 ,可得
 (23) (23)
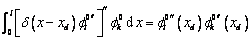 (24) (24)
于是式(22)可进一步简化为
 (25) (25)
根据 和 和 的两种情况,可分别求得 的两种情况,可分别求得
 (26) (26)
 (27) (27)
与式(17)相似,可将二阶摄动 表示成完整梁振型 表示成完整梁振型 (j=1,2,3,···)的线性组合 (j=1,2,3,···)的线性组合
 (28) (28)
式中, 为二阶摄动项的线性组合系数。 为二阶摄动项的线性组合系数。
略去复杂的推导,可得式(14)的解为
  (29) (29)

 (30) (30)
将式(26)、(29)代入式(10),将式(27)、(28)、(19)、(28)代入(11),可求得受损简支梁的特征值和模态振型。
4 受损简支梁的模态振型和模态曲率
将简支梁按梁长进行归一化处理,取结构参数:l=1.0m、b=0.03m、h=0.03m、xd=0.5m,取材料特性参数(混凝土):E=20GPa、ρ=2400kg/m3,取裂纹损伤参数:ε=0.2、?l=0.002m。
4.1 受损梁的固有频率
表1 完整梁和损伤梁的前4阶固有频率
Table 1 Former 4order natural frequencies of the intact and damaged beam
|
阶次
|
1
|
2
|
3
|
4
|
|
固有
频率
/Hz
|
完整梁
|
246.74
|
986.96
|
2220.66
|
3947.84
|
|
损伤梁(展开至ε)
|
246.56
|
986.69
|
2220.05
|
3944.99
|
|
变动量(展开至ε)
|
0.18
|
0.27
|
0.61
|
2.86
|
|
损伤梁(展开至ε2)
|
246.56
|
986.68
|
2220.04
|
3944.94
|
|
变动量(展开至ε2)
|
0.18
|
0.26
|
0.62
|
2.90
|
完整梁和受损梁的固有频率可分别由式(18)和 求得,前4阶振型的固有频率见表1。从表1可以看出,在微小损伤的条件下摄动方法,相对于损伤前的固有频率,梁的固有频率的一阶和二阶变动量都非常小。也就是说,当结构测量时存在噪声的情况时,单纯地希望从梁体的固有频率变化来识别微小的损伤,来获取识别正确结果是比较困难的。另外从表1还可以看出,按式(10)展开到一阶摄动量ε和二阶摄动量ε2,固有频率的结果非常接近。 求得,前4阶振型的固有频率见表1。从表1可以看出,在微小损伤的条件下摄动方法,相对于损伤前的固有频率,梁的固有频率的一阶和二阶变动量都非常小。也就是说,当结构测量时存在噪声的情况时,单纯地希望从梁体的固有频率变化来识别微小的损伤,来获取识别正确结果是比较困难的。另外从表1还可以看出,按式(10)展开到一阶摄动量ε和二阶摄动量ε2,固有频率的结果非常接近。
4.2 受损梁的模态振型和模态曲率
取裂缝损伤位置xd=0.4l,绘制了损伤简支梁的前4阶的归一化模态振型和模态曲率沿l的分布曲线,如图2和图3所示中国学术期刊网。
比较图2和图3的(a)和(b)可以发现,展开到一阶摄动量ε和二阶摄动量ε2得到的曲线非常接近,一般情况下,展开到一阶摄动量ε基本上能满足精度要求。
从图2可以看出,当存在微小的裂缝损伤时,损伤点处的模态振型都是相当光滑的,和损伤前的模态振型基本上一致。相比之下,图3中损伤点处的模态曲率出现了比较明显的变化,不再像图2那样是光滑的,出现这种现象的原因在于:由式(11)可以看出,在损伤条件一定的情况下,模态曲率的变化量与完整梁的 有关,而根据式(16)可得 有关,而根据式(16)可得 , , 与 与 的数值相反,而且 的数值相反,而且 的数值是 的数值是 的 的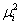 倍,于是随着阶次的增高, 倍,于是随着阶次的增高,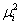 值越大,模态曲率的变动量越来越显著。 值越大,模态曲率的变动量越来越显著。

(a) 展开到一阶摄动量ε
(a) Computed to first order perturbation ε

(b) 展开到二阶摄动量ε2
(b) Computed to second order perturbation ε2
图2 损伤梁的前4阶模态振型
Fig. 2 Former 4 order modal shape of damaged beam

(a) 展开到一阶摄动量ε
(a) Computed to first order perturbation ε

梁长l /m
(b) 展开到二阶摄动量ε2
(b) Computed to second order perturbation ε2
图3 损伤梁的前4阶模态曲率
Fig. 3 Former 4 order modal curvature of damaged beam
为了更好地分析损伤简支梁的曲率变化,绘制了前4阶的模态曲率的变动量沿l的分布曲线,如图4所示。
比较图4(a)和(b)可以发现,两曲线反映的规律完全一致,即随着阶次的增高,模态曲率的变动量越来越大,而且曲率的峰值点正好对应于损伤位置摄动方法,这也印证了很多文献中提出的观点[10,11]:即用模态曲率进行梁结构的损伤识别,识别效果要优于直接用模态振型。对于前3阶模态曲率,两曲率曲线非常接近,但对于第4阶模态曲率,图4(b)的最大数值明显要高于4(a),这主要是因为模态阶数越高,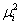 值越大,由此产生的模态曲率也越大。 值越大,由此产生的模态曲率也越大。

(a) 展开到一阶摄动量ε
(a) Computed to first order perturbation ε

(b) 展开到二阶摄动量ε2
(b) Computed to second order perturbation ε2
图4 损伤梁的前4阶模态曲率的变动量
Fig. 4 Variations of the former 4 order modal curvature of damagedbeam
5 结 论
本文采用摄动理论将裂纹损伤表示成二阶摄动,得到了受损简支梁的固有频率、模态振型和模态曲率的解析式,并进行了数值计算,得到以下主要结论:
(1) 当损伤程度较低时,损伤梁的固有频率和模态振型与完整梁非常接近,即从固有频率和模态振型的变化无法判断简支梁损伤与否,更无法判断损伤的具体位置;
(2) 根据损伤与完整简支梁模态曲率的变动量(即差值)的峰值可以明显地判断出损伤位置,峰值随着模态阶数的增大而增大;
(3) 模态阶数低于三阶时,将损伤展开到二阶摄动和一阶摄动的模态曲率基本接近,但随着阶数的增大,前者计算的模态曲率峰值要高于后者。
参考文献:
[1]谢峻,韩大建.一种改进的基于频率测量的结构损伤识别方法[J]. 工程力学, 2004, 21 (1): 21-25. (Xie J, Han D J. An improved methodfor structure damage detection based on frequency measurement[J]. EngineeringMechanics, 2004, 21 (1): 21-25 (in Chinese). )
[2]Salawu O S. Detection of structuraldamage through changes in frequency: a review[J]. Engineering Structures, 1997,19(9): 718-723.
[3]Palacz M., Krawczuk M. Vibrationparameters for damage detection in structures[J]. Journal of Sound and Vibration,2002, 249(5): 999-1010.
[4]王山山,任青文.基于曲率模态振型的刚架结构损伤检测[J]. 动力学与控制学报, 2005, 3(2): 81-86. (Wang S S, Ren Q W. Damage detection forframe structure using curvature mode shapes[J]. Journal of Dynamics andControl, 2005, 3(2): 81-86 (in Chinese). )
[5]Pandey M B., Samman M M. Damagedetection from changes in curvature mode shapes[J]. Journal of Sound andVibration, 1991, 145(2): 321-332.
[6]Abdel Wahab MM,De Roeck G. Damagedetection in bridges using modal curvatures :application to a real damage scenario[J].Journal of Sound and Vibration,1999, 226 (2): 217-235.
[7]陈江义,陈花玲,王永泉.用摄动方法进行受损悬臂梁的模态分析[J]. 中国机械工程, 2005, 16(3): 209-211.(Chen J Y, Chen H L, Wang Y Q. Modal analysis of damaged cantilever-beam using perturbationmethod[J]. China Mechanical Engineering, 2005, 16(3): 209-211 (in Chinese). )
[8]唐友刚.高等结构动力学[M]. 天津: 天津大学出版社, 2002. ( Tang Y G.Advanced structure dynamics[M]. Tianjin, Tianjin University Press, 2002 (inChinese). )
[9]陈塑寰.结构动态设计的矩阵摄动理论[M]. 北京: 科学出版社, 1999. (Chen S H. Matrixperturbation theory structural dynamic design[M]. Beijing: Science Press, 1999(in Chinese). )
[10]Pandey A K, Biswas M, Samman M M. Damage Detection fromChanges in Curvature Mode Shapes. Journal of Sound and Vibration, 1991, 145:312-332.
[11]Abdelwahab M M. Effect of Modal Curvature on DamageDetection Using Model Updating. Mechanical Systems and Signal Processing, 2001,15(2): 439-445.
2/2 首页 上一页 1 2 |


