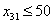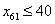 , , , , , ,
 , , , , , ,
 , , , , , ,
 , , , , , ,
 , , ,
 
 皆为整数
取 ，然后利用Lingo软件[3]编程求解，根据求解得出的结果得到了各宾馆预订房间信息如下表（表3）：
表3 各宾馆预订房间信息
|
宾馆序号
|
房间规格
|
房间间数
|
价格（天）
|
安排房间数目
|
|
1
|
普通双标间
|
50
|
180元
|
50
|
|
商务双标间
|
30
|
220元
|
30
|
|
普通单人间
|
30
|
180元
|
30
|
|
商务单人间
|
20
|
220元
|
20
|
|
2
|
普通双标间
|
50
|
140元
|
50
|
|
商务双标间
|
35
|
160元
|
35
|
|
豪华双标间A
|
30
|
180元
|
30
|
|
豪华双标间B
|
35
|
200元
|
35
|
|
3
|
普通双标间
|
50
|
150元
|
50
|
|
商务双标间
|
24
|
180元
|
0
|
|
普通单人间
|
27
|
150元
|
27
|
|
4
|
普通双标间
|
50
|
140元
|
0
|
|
商务双标间
|
45
|
200元
|
1
|
|
7
|
普通双标间
|
50
|
150元
|
50
|
|
商务单人间
|
40
|
160元
|
27
|
|
商务套房(1床)
|
30
|
300元
|
0
|
|
9
|
普通单人间
|
30
|
260元
|
22
|
|
合计
|
|
457
|
从上表容易看出，共需要安排6间宾馆住宿，为1、2、3、4、7、9号。有些宾馆需要的客房数量很少，可考虑调整其它有入住代表的宾馆内，使得宾馆数量尽可能减少。由于4号宾馆只安排了1间房，根据题中附表2的价位范围可调整至3号宾馆商务双标间中；同理，9号宾馆中22间房可移至7号商务套房（1床）中。通过调整，得到结果如下表（表4）：
表4 各宾馆预订房间信息（调整后）
|
宾馆序号
|
房间规格
|
房间间数
|
价格（天）
|
安排房间数目
|
|
1
|
普通双标间
|
50
|
180元
|
50
|
|
商务双标间
|
30
|
220元
|
30
|
|
普通单人间
|
30
|
180元
|
30
|
|
商务单人间
|
20
|
220元
|
20
|
|
2
|
普通双标间
|
50
|
140元
|
50
|
|
商务双标间
|
35
|
160元
|
35
|
|
豪华双标间A
|
30
|
180元
|
30
|
|
豪华双标间B
|
35
|
200元
|
35
|
|
3
|
普通双标间
|
50
|
150元
|
50
|
|
商务双标间
|
24
|
180元
|
1
|
|
普通单人间
|
27
|
150元
|
27
|
|
7
|
普通双标间
|
50
|
150元
|
50
|
|
商务单人间
|
40
|
160元
|
27
|
|
商务套房(1床)
|
30
|
300元
|
22
|
|
合计
|
|
457
|
调整后的宾馆间数为4，分别为1、2、3、7号宾馆，从题附图的各宾馆的地理位置上来看，这4间宾馆位置距离上还算集中。
由于与会代表人数只是估算出来的，与实际人数有出入，若预定客房的数量大于实际用房数量数学建模，则需要支付一天的空房费，而若出现预定客房数量不足，则将造成非常被动的局面，引起代表的不满。权衡两者之间，应首先考虑的是代表满意度情况，所以筹备组可以在所预定宾馆内再相应预定一些空房，作为备用。
3模型的讨论
3.1 模型的优点
（1）本模型的建立使问题简单化，实用性强，与所了解到事实相符；
（2）所用知识比较初等，解决问题的方法比较易于理解；
（3）使用Matlab6.5，Lingo8进行求解、画图较便捷；
（4）使用表格和图形对数据进行分析，使读者一目了然。
3.2 模型的缺点
（1）少量数据的变化对模型的结果影响较大。
（2）没有对代表满意度进行具体的量化分析。
参考文献
[1]全国大学生数学建模竞赛.2009年赛题[OL].[2011-02-10].http://mcm.edu.cn/
html_cn/node/50a7a9fc36c5ce6fd242dbbc1da5878e.html.
2/2 首页 上一页 1 2 |
