基于多目标规划的会议筹备模型设计_数学建模

论文导读:：针对2009年全国大学生数学建模竞赛D题――“会议筹备”中的有关数据进行综合分析，以选择的宾馆数量最少、宾馆间距离上最靠近为两个目标函数，同时考虑与会代表在价位、是否独住两方面的约束，通过采用多目标规划进行问题建模并求解来制定一个预定宾馆客房的合理方案。
论文关键词：数学建模，曲线拟合，多目标规划

 

1问题的提出及分析

针对2009年全国大学生数学建模竞赛D题^[1]――“会议筹备”中如何制定预定宾馆客房的合理方案的问题，综合考虑经济、方便、代表满意等方面来建立优化模型，具体主要从与会代表的价位需求、所选宾馆的数量和距离来分析，采用多目标规划进行问题建模与求解。

2模型的建立与求解

2.1数据的处理

首先根据问题提供的数据信息来估算与会的代表的人数。

设为发来回执的代表数量，为发来回执但未与会的代表数量，为未发回执与会的代表数量，根据题中附表3的信息且利用Matlab软件^[2]的曲线拟合可以得出与的函数关系为：。用此函数拟合的效果如图1所示：

图1 发来回执但未与会的代表数量与发来回执的代表数量

之间的曲线拟合图

也可得出与的函数关系为：。曲线拟合如下图（图2）：

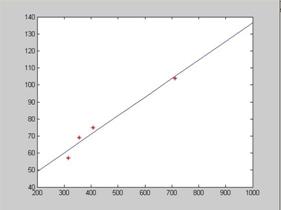
图2 未发回执与会的代表数量与发来回执的代表数量

之间的曲线拟合图

利用题中附表2的信息可计算出本届发来回执的代表数量为755人，利用上面所得出的拟合函数，可估算出本届发来回执但未与会的代表数量为：，

本届未发回执而与会的代表数量为：，故本届与会代表的数量可估算为：。

根据附表2由此可以估算与会代表有关住房要求的信息（单位：人）数学建模，如下表（表1）：表1 与会代表人数及需要的房间数

2.2 模型的分析

假设为需要第号宾馆第种规格的数量（比如需要1号宾馆普通双标间的数量记为），为需要第号宾馆的房间总数，为0-1变量，表示第号宾馆是否被预订，若被预订则为1，否则为0。即

，

由于预计会议规模庞大，而适于接待这次会议的几家宾馆的客房和会议室数量均有限，所以只能让与会代表分散到若干家宾馆住宿。结合实际，主要制定合理的预定宾馆客房的方案，以满足两个需求因素：目标1：选择的宾馆数量最少；目标2：宾馆间距离上最靠近。

目标分析：

在保证选择的宾馆数量尽可能少的同时，对距离也要求比较靠近。

目标1可表示为:

（1）

根据题中附图可统计出10间宾馆各间宾馆之间的乘车距离，如下表（表2）：

表2 各宾馆间的乘车距离（单位：米）

为了满足距离上最靠近，可考虑入住宾馆各间之间的距离之和达到最小。
 

假设为第i间宾馆与第j间宾馆之间的距离。易知，。则目标2可表示为：

（2）

其中为第i间宾馆与第j间宾馆之间的距离论文参考文献格式。

约束分析：

与会代表回执中不仅对每间住房有价格上的要求，而且也同时要求合住或独住。价格上分每天每间120～160元、161～200元、201～300元三种不同的价格，合住是指要求两人合住一间，独住是可安排单人间，或一人单独住一个双人间。

因此，在安排住房时，应先考虑双人合住的数量。故有如下约束：

① 合住1和独住1满足的总房间数

； （3）

满足合住1的房间数；（4）

②合住2和独住2满足的总房间数

； （5）

满足合住2的房间数； （6）

③合住3和独住3满足的总房间数

；（7）

满足合住3的房间数；（8）

其中，为需要第号宾馆第种规格的数量。

2.3 模型的建立与求解

基于2.2的分析数学建模，以（1）（2）为目标，以（3）~（8）为约束，建立多目标规划模型，其求解可采用多属性效用函数，将多目标规划模型转化为单目标规划模型来求解。

首先，考虑到模型中的2个目标函数都是要求最小化，因此运用线性加权法将多目标规划模型化为单目标规划模型来求解，加权得到的优化模型如下所示：

,,,

,,,,

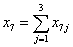 1/2    1 2 下一页 尾页