其中θ为表面编织角,a为内部编织角,β为角编织角。根据纤维束的空间结构可推算出内部单胞、表面单胞和角单胞各自的纤维体积 、 、 和 和 以及各自单胞的体积 以及各自单胞的体积 、 、 和 和
 (5) (5)
![三维编织复合材料几何建模及数值分析[*] 弹性性能](/d/file/picture/201105/29/1.files/image037.gif) (6) (6)
 (7) (7)
![三维编织复合材料几何建模及数值分析[*] 弹性性能](/d/file/picture/201105/29/1.files/image039.gif) (8) (8)
 (9) (9)
 (10) (10)
其中 为单胞内纤维束沿中心迹线的长度 为单胞内纤维束沿中心迹线的长度
 (11) (11)
图3 表面单胞图4 角单胞
3 周期性位移边界条件
含周期性单胞的材料在外载荷作用下,其应力应变场应呈现出周期性和连续性。因此,对单个周期性单胞的分析应在周期性边界条件下进行,以得到单胞合理的细观应力分布。
对于含周期性单元胞体的结构,其边界面上的位移场可表示为[14]
 (12) (12)
其中 为平均应变, 为平均应变, 为线性分布位移场, 为线性分布位移场, 为边界面上的周期性位移修正分量。对由周期性代表单元组成的材料,相邻单胞边界处应满足2个连续性条件:(1)位移连续,即变形后在相邻单胞边界处不能出现间隙或相互嵌入;(2) 应力连续,即在周期性单胞相对平行面的应力一致。显然,式(12) 满足位移连续条件单胞,但由于 为边界面上的周期性位移修正分量。对由周期性代表单元组成的材料,相邻单胞边界处应满足2个连续性条件:(1)位移连续,即变形后在相邻单胞边界处不能出现间隙或相互嵌入;(2) 应力连续,即在周期性单胞相对平行面的应力一致。显然,式(12) 满足位移连续条件单胞,但由于 通常为一未知量,很难直接用于实际建模分析。 通常为一未知量,很难直接用于实际建模分析。
对于周期性单胞而言,单胞边界面通常是成对且平行出现,相应平行边界面上的位移场可以写成
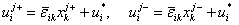 (13) (13)
式中,符号 和 和 分别表示单胞的第 分别表示单胞的第 组相对平行面,而在周期性单胞相对平行面的对应点上, 组相对平行面,而在周期性单胞相对平行面的对应点上, 是一致的,由式(13)得 是一致的,由式(13)得
 (14) (14)
式中,对单胞每组相对平行面而言, 为一常数,一旦给定 为一常数,一旦给定 ,等式右侧位移差即为常值。式(14) 对应节点位移差在数值分析中可直接通过施加相应节点位移线性约束方程实现, 从而回避了直接给出周期性单胞的实际位移边界值。 ,等式右侧位移差即为常值。式(14) 对应节点位移差在数值分析中可直接通过施加相应节点位移线性约束方程实现, 从而回避了直接给出周期性单胞的实际位移边界值。
可以证明[15],只要采用基于位移元建立的单胞有限元模型,施加式(14)所给定的位移差边界,就足以保证求解的惟一性,并使表面应力连续性得以自然满足,即
 (15) (15)
在小变形情况下,可认为周期性单胞为线弹性各向异性体,其本构方程为
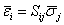 (16) (16)
式中 为单胞等效柔度矩阵; 为单胞等效柔度矩阵; 、 、 分别为单胞宏观平均应变和平均应力,其定义为 分别为单胞宏观平均应变和平均应力,其定义为
 (17) (17)
由式(16)可知,一旦给定6 组不相关的位移边界条件 ,即可分别求出每种工况下的平均应力 ,即可分别求出每种工况下的平均应力 ,得到总共6组方程。求解这不相关的6组方程,从而确定单胞等效柔度矩阵 ,得到总共6组方程。求解这不相关的6组方程,从而确定单胞等效柔度矩阵 。对于矩形单胞而言 。对于矩形单胞而言
 (18) (18)
其中: 为单胞的第 为单胞的第 面; 面; 为第 为第 面上所有节点 面上所有节点 方向节点力之和。 方向节点力之和。
4 数值算例
为验证本文模型的合理有效性单胞,与实验结果进行了比较毕业论文开题报告。根据Chen[16] 所提供的三维四步 编织复合材料试件的参数(碳纤维/环氧树脂),计算了材料单胞在周期性边界条件下的等效弹性性能。材料组分性能参数见表1,试件工艺参数及单胞模型结构参数见表2。 编织复合材料试件的参数(碳纤维/环氧树脂),计算了材料单胞在周期性边界条件下的等效弹性性能。材料组分性能参数见表1,试件工艺参数及单胞模型结构参数见表2。
表1 组分性能参数
|
材料
|
弹性模量/GPa
|
泊松比
|
|
Ef1
|
Ef2
|
Gf12
|
Gf23
|
μf12
|
μm
|
|
碳纤维
|
230
|
40
|
24
|
14.3
|
0.25
|
|
|
环氧树脂
|
3.5
|
|
|
|
|
0.34
|
表2 试样工艺参数及单胞模型结构参数
|
工件
|
试样工艺参数
|
单胞模型结构参数
|
|
Dy/m
|
a(o)
|
Vf /%
|
尺寸/mm
|
γ(o)
|
a/mm
|
b/mm
|
Wx=Wy
|
h/mm
|
φ/%
|
|
1
|
0.757
|
19.0
|
46.6
|
20×6×250
|
26.0
|
0.599
|
0.385
|
2.175
|
6.317
|
0.578
|
|
2
|
0.757
|
30.0
|
47.2
|
20×6×250
|
39.0
|
0.542
|
0.404
|
2.286
|
3.960
|
0.607
|
|
3
|
0.757
|
37.0
|
47.1
|
20×6×250
|
46.8
|
0.503
|
0.425
|
2.402
|
3.188
|
0.623
|
基于本文几何建模思路,对各试件单胞分别施加表3所示周期性位移边界工况。表4给出了弹性常数的数值预报结果及实验数据。由表可知,模型弹性常数预测值与实验吻合较好,表明了该细观几何模型的有效性。同时,各试件具有几乎相等的纤维体积含量,随着试件1到试件3编织角的增大,轴向模量 迅速减小,横向模量 迅速减小,横向模量 和 和 逐步增大, 但增幅有限;剪切模量 逐步增大, 但增幅有限;剪切模量 、 、 、 、 增幅较为明显。弹性模量随编织角的变化趋势与基于层板的理论模型基本一致,进一步证明了本文数值模型的合理性。 增幅较为明显。弹性模量随编织角的变化趋势与基于层板的理论模型基本一致,进一步证明了本文数值模型的合理性。
表3 单胞周期性位移边界条件
|
工况 k
|
εx
|
εy
|
εz
|
γyz
|
γzx
|
γxy
|
|
1
|
0.01
|
0
|
0
|
0
|
0
|
0
|
|
2
|
0
|
0.01
|
0
|
0
|
0
|
0
|
|
3
|
0
|
0
|
0.01
|
0
|
0
|
0
|
|
4
|
0
|
0
|
0
|
0.02
|
0
|
0
|
|
5
|
0
|
0
|
0
|
0
|
0.02
|
0
|
|
6
|
0
|
0
|
0
|
0
|
0
|
0.02
|
表4 试件弹性常数数值结果与实验对比
|
工程弹性常数
|
No. 1
|
No. 2
|
No. 3
|
|
实验值
|
本文预测值
|
实验值
|
本文预测值
|
实验值
|
本文预测值
|
|
Ex /GPa
Ey /GPa
Ez /GPa
Gxy /GPa
Gyz /GPa
Gxz /GPa
μxy
μyz
μxz
|
58.74
0.72
0.69
|
8.57
8.57
57.33
11.24
11.24
4.08
0.37
0.70
0.69
|
27.60
0.78
1.00
|
8.69
8.69
26.07
15.23
15.23
8.57
0.31
0.70
0.82
|
18.05
0.80
0.72
|
10.01
10.01
17.47
16.63
16.63
11.29
0.32
0.77
0.70
|
5 结论
本文根据三维编织复合材料中纤维束的实际空间几何结构建立了比较合理的三胞模型。模型中不仅考虑了3种单胞各自纤维束的空间结构,还考虑了3种单胞中纤维束的弯曲及纤维束的不同截面形状对材料弹性常数的影响。应用本文的几何分析模型, 并引入周期性位移边界条件,建立了编织复合材料有效弹性常数的数值预报模型。不同尺寸试件的数值预报结果和实验结果比较吻合,从而验证了本文模型的有效性以及普适性。
参考文献
1.Whitney T J, Chou TW, Modeling of 3-Dangle-interlock textile structural composite, Journal of Composite Material. 1989,23(9): 890-91
2.Crane R M, Camponeschi E T, Experimentaland analytical characterization of multi-dimensionally braided graphite/epoxycomposites. Experiment Mechanics, 1986, 19: 259-266.
3.梁军,三维编织复合材料力学性能的细观研究.哈尔滨:哈尔滨工业大学博士学位论文,1996年.
4.梁军,杜善义,韩杰才.一种含特定微型纹缺缺陷三维编织复合材料弹性常数预报方法.复合材料学报,1999,16(3):135-139.
5.Ma, Chang-Long, Jean-Ming Yang andTsu-Wei Chou. Elastic stiffness of three-dimensional braided textile structurecomposites. ASTM STP 893. Composite Materials: Testing and Design, Philadelphia, 1986: 404-421.
6.Yang JM, Ma CL and Chou TW, FiberInclination Model of Three Dimensional Textile Structural Composites. Journalof Composite Material, 1986, 20(1): 472-484.
7.Wu DL, Three-cell model and 5-D braidedstructural composites. Composites Science and Technology, 1996, 56: 225-233.
8.严实,吴林志等,三维四向编织复合材料有效性能的预报.复合材料学报,2007,24(1):158-166.
9.王兵,吴林志等,碳纤维增强金字塔点阵夹芯结构的抗压缩性能.复合材料学报,2010,27(1):133-138.
10.Kalidindi SR, Franco E. Numericalevaluation of iso strain and weighted-average models for elastic moduli of there-dimensional composites. Composites Science and Technology, 1997, 57(3):293-305.
11.Sun X K, Sun C J Mechanical propertiesof t here-dimensional braided composites. Composite Structures, 2004, 65 (3/4):485-492.
12.陈利,三维编织复合材料的细观结构及其弹性性能分析.天津:天津纺织工学院博士学位论文,1998年.
13.Whyte DE,PaStore CM, Ko F K, A fabric geometry model for 3-D braid reinforced FP/AI-Licomposites. In: Inter SAMPE Metals Cont, Competitive Advances in Metals/MetalProcessing, CherryHill, Aug. 1987: 87-21.
14.Suquet P. Elements of homogenization theory for inelastic solid mechanics.∥Sanchez-Palencia E , Zaoui A. Homogenization Techniques forComposite Media. Berlin: Springer-Verlag,1987: 194-275.
15.Xia ZH, Zhou CW, Yong QL , et al. Onselection of repeated unit cell model and application of unified periodicboundary conditions in micro-mechanical analysis of composites. InternationalJournal of Solids and Structures , 2006 , 43: 266-278.
16.Chen L, Tao XM, Choy CL, Mechanicalanalysis of 3D braided composites by the multiphase element method. CompositesScience and Technology, 1999, 59(16): 2383-2391.
2/2 首页 上一页 1 2 |


