论文摘要:采用了航材保障良好率作为航材保障的效能指标,建立了航材保障良好率的数学模型。以航材保障经费为资源,平均航材保障良好率达到最大为目标函数,建立了航材保障经费的优化配置模型,用动态规划的顺序解法求解,并建立了最优递推方程。将配置模型应用于实例,计算工具是Matlab, 进行了数值实验和理论分析,结果证明该模型的优化效果和实用性很好。
论文关键词:优化配置,效能指标,动态规划,航材保障良好率,数学模型
引言
航材保障的目的是为飞机及其备件维修提供所需器材,确保飞机飞行安全可靠,其基本任务是及时、准确、经济地供应部队所需的航材,保证作战训练任务的完成。随着高新技术的不断采用,飞机及其备件的购置费用已十分昂贵,为保障飞机正常使用所需要的费用,更是以惊人的速度增长。一些统计资料表明,在飞机及其备件的寿命周期费用中,飞机的维修保障费用约占50%~80%。但是,航材保障经费的增长却很有限,因此,如何利用有限的航材保障经费最大限度地提高航材保障系统的整体效能成为一项重要的课题。
1航材保障效能指标的选择
目前,关于航材保障经费的优化配置已经有一定的研究,但是其模型所选择的效能指标(即在场良好飞机架日)不合理。
效能指标作为系统优化的决策依据或系统的评价标准,对系统研究的成败具有决定意义。在军事效能评估实践中,不乏这样的实例,即由于选用了不恰当的效能指标而使效能评估研究得出错误结论。例如,第二次世界大战期间英国商船安装高炮,若用高炮击落飞机概率作为效能指标,则效能几乎为零。但是,若用商船损失概率作为评价指标,则损失概率由25%下降到10%,说明安装高炮效能相当高。
航材保障经费配置的目标是将有限的经费合理地配置以最大限度地提高航材保障系统的整体保障效能,所以其模型建立的关键就是选择能够有效度量航材保障效能的指标。航材保障效能描述了在一定条件下,航材保障系统被用来完成保障任务所能达到预期目标的程度,是航材保障系统在保障过程中其保障能力发挥的效果,是对航材保障能力和航材保障军事效益的综合考虑。在场良好飞机架日只能反应出航材保障能力的高低,不能反应出航材保障军事效益的多少,因此其配置方案也不是最优。正确的方法是采用航材保障良好率作为配置模型的效能指标,其定义如下:

其中,在场良好飞机架日=在场飞机总架日-因缺航材停飞架日。
显然,与在场良好飞机架日相比,航材保障良好率能够有效地度量投入一定航材经费时的任务完成程度以及所产生的军事效益,同时,它也是航材保障指挥部门对航材保障经费进行预测的重要指标。因此,下面就采用航材保障良好率建立航材保障经费的配置模型,其目标是使各单位的平均航材保障良好率达到最大。
2航材保障经费配置模型的建立
设某舰航下辖n个场站,x为分配给第i个场站的经费,g(x)为第i个场站获得x单位经费所达到的航材保障良好率;W为舰航的航材保障经费,其所辖场站的平均航材保障良好率为z,以z达到最大为目标,则航材保障经费的配置模型为:
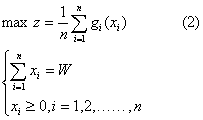
其中,航材保障良好率的高低与航材保障经费的投入存在一定的规律,即航材保障经费投入越多航材保障良好率越高。但是随着航材保障经费的增加,航材保障良好率的增量逐渐减少。显然,航材保障经费服从以航材保障良好率的增量为概率密度的正态分布,其分布函数就是航材保障良好率,即

其中,μ、σ为第i个场站所得经费的期望和标准差。
3用动态规划法求解经费配置模型
航材保障经费配置模型以航材保障经费为资源、以平均航材保障良好率达到最大为目标,是一个典型的一维资源配置问题,可以用动态规划法求解。
动态规划法是解决多阶段决策过程最优化的一种数学方法,产生于20世纪50年代,由美国数学家贝尔曼等人提出。依据贝尔曼最优原理:对最优策略来说,无论过去的状态和决策如何,由前面诸策略所形成的状态出发,相应的剩余决策序列必构成最优子策略。对航材保障经费配置模型进行离散分步求解,即可快速求出优化数据。
用边际分析法也可以求出最优解,但是与动态规划法相比,边际分析法在某些情况下(如求装备备件最优库存)不能获得所有整数费用值下的最优解,所以对经费的预测能力不足,适用性不如动态规划法。
动态规划法通常把资源分配给一个或几个使用者的过程作为一个阶段,把问题中的一次分配给某个使用者的资源作为决策变量,将累计的量或随递推过程变化的量作为状态变量。
下面将问题按场站分为n个阶段,分别编号为1、2、……、n。
状态变量s表示分配给前i个场站的经费;决策变量即为航材保障良好率模型中的x;状态转移方程为s=s-x,表示分配给前i-1个场站的经费;允许决策集合为D={x|0≤x≤s}。
令f(s)为前i个场站获得s单位经费所达到的航材保障良好率总和,则f(s)为前i-1个场站获得s单位经费所达到的航材保障良好率总和。
另外,实际工作中,航材保障必须达到一定的航材保障良好率,所以求解时为了减少不必要的计算,可以给各场站均配置一定的初始经费x,仅对剩余经费进行优化配置,但计算航材保障良好率时则要包含初始经费。
综上所述,根据动态规划的顺序解法,该模型的最优递推方程为:

此时有

4实例分析
设某舰航下辖六个场站,根据历年统计数据计算出的航材保障经费的期望和标准差如表1所示(单位:万元)。 1/2 1 2 下一页 尾页 |


