令 ,则 ,则 ; ;
令 ( ( ≥ ≥ 为奇素数),则 为奇素数),则 . .
综上,定理 得证. 得证.
再证定理 .根据引理 .根据引理
令 ( ( 为非负整数),则 为非负整数),则
 ; ;
令 ( ( 为非负整数),则 为非负整数),则
 ; ;
令 ( ( 为非负整数, 为非负整数, 为奇素数),则 为奇素数),则
 ; ;
令 ( ( 为大于 为大于 的正整数, 的正整数, 为适合 为适合 的奇素数),则 的奇素数),则
 ; ;
令 ( ( 为正整数, 为正整数, 、 、 为不同的奇素数),则 为不同的奇素数),则
 ; ;
令 ( ( 为大于 为大于 的素数),则 的素数),则
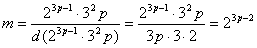 ; ;
令 ( ( 为非负整数, 为非负整数, 为大于 为大于 的素数),则 的素数),则
 ; ;
令 ( ( 为非负整数, 为非负整数, 为奇素数),则 为奇素数),则
 . .
综上,定理 得证. 得证.
由定理 很容易算出在1—100的范围内,当 很容易算出在1—100的范围内,当 1,2,3,4,5,7,8,9,11,12,13,15,16,17,18,19,20,21,23,24,26,27,29,30,31,32,35,36,37,38,39,40,41,42初等方法,43,45,47,48,49,50,51,52,54,55,57,59,62,64,65,66,67,69,71,72,74,77,79,81,82,83,84,85,87,88,89,90,91,92,95,96,98,99时, 1,2,3,4,5,7,8,9,11,12,13,15,16,17,18,19,20,21,23,24,26,27,29,30,31,32,35,36,37,38,39,40,41,42初等方法,43,45,47,48,49,50,51,52,54,55,57,59,62,64,65,66,67,69,71,72,74,77,79,81,82,83,84,85,87,88,89,90,91,92,95,96,98,99时, 都是优美指数.于是我们猜测:若 都是优美指数.于是我们猜测:若 6,10,14,22,25,28,33,34,44,46,53,56,58,60,61,63,68,70,73,75,76,78,80,86,93,94,97,100,则 6,10,14,22,25,28,33,34,44,46,53,56,58,60,61,63,68,70,73,75,76,78,80,86,93,94,97,100,则 都不是优美指数,从而进一步猜测:存在无穷多个正整数不是优美指数. 都不是优美指数,从而进一步猜测:存在无穷多个正整数不是优美指数.
参考文献
[1]Murthy A..Some more conjectures on primes and divisors[J].Smarandache
NotionsJ,2001(12):311-312.
2/2 首页 上一页 1 2 |


