
当且仅当 相互独立时(1)式等号成立。 相互独立时(1)式等号成立。
由(1)式可以推出无论资产损失率分布是否呈现正态分布, 都是具有有一致性的风险度量,且其具有次可加性,能够满足在分布呈高维下 都是具有有一致性的风险度量,且其具有次可加性,能够满足在分布呈高维下 处理不足的情况,同时能够简单明了的说明对于任意几个单项投资 处理不足的情况,同时能够简单明了的说明对于任意几个单项投资 来说,其投资组合 来说,其投资组合 的风险损失明显小于单项投资损失之和,这就和经典分散投资理论相吻合。 的风险损失明显小于单项投资损失之和,这就和经典分散投资理论相吻合。
由(2)式可以推断出 具有凸性,它可以简单有效的计量当数据量很大时的风险损失情况从而弥补了在计量数据量较大时 具有凸性,它可以简单有效的计量当数据量很大时的风险损失情况从而弥补了在计量数据量较大时 计量带来的不足。 计量带来的不足。
此外当损失分布呈正态分布时容易证明其 贝叶斯估计, 贝叶斯估计, 以及均值—方差理论在计量风险损失方面具有相同的最优解。 以及均值—方差理论在计量风险损失方面具有相同的最优解。
从以上的说明中可以看出在计量风险损失方面 比 比 具有更好的适用性期刊网。 具有更好的适用性期刊网。
(三) 与 与 的数学关联性 的数学关联性
通过计算两者之间的算术表达等式可以进一步的说明 与 与 之间的关系。 之间的关系。

又由

其中 ,故我们可得: ,故我们可得:
 (5) (5)
其中 。 。
二.贝叶斯方法在损失分布中的应用
现在我们一般应用的风险管理模型,常常采用计算机模拟的方法去拟合损失分布,常存在比较严重的失真现象,即拟合的分布与实际的情况之间总是会存在或多或少的差异,比如以前我们对于市场风险的资产损失分布是假设其服从正态分布的,但随着各种较大风险的发生通过研究逐渐发现其分布实际是具有后尾特征的(其发生风险的概率要远远大于正态分布假设下认定的概率)。因此为了提高准确性,我们就要利用各种有用的信息来提高精度。
本文先利用历史数据对各个参数进行正态拟合,得到正态分布下各个参数的修正值,并且以此作为各个参数的先验分布,然后通过历史样本数据对其各个参数再进行贝叶斯修正,得到各参数的后验分布,进而就能得到各参数比较精确的估计值[7][8]。
(一) 的贝叶斯修正 的贝叶斯修正
由市场风险损失的历史数据( ), ), ,为计算方便起见我们不妨假设 ,为计算方便起见我们不妨假设 是已知的,且其值为 是已知的,且其值为 。这样通过抽样可以得到样本的似然函数: 。这样通过抽样可以得到样本的似然函数:
 (6) (6)
实际的计算过程中可以根据历史数据结合最大似然估计等方法用最小方差无偏估计来做为已知 的值,或者可以直接应用经过贝叶斯修正以后的 的值,或者可以直接应用经过贝叶斯修正以后的 值。 值。
已知正态分布中的 的共轭先验分布的形式为倒伽马分布贝叶斯估计,Gamma分布的密度函数为: 的共轭先验分布的形式为倒伽马分布贝叶斯估计,Gamma分布的密度函数为:
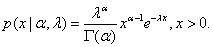 (7) (7)
由此可得 共轭先验分布的分布密度函数 共轭先验分布的分布密度函数 ,其中 ,其中 与 与 为已知。 为已知。
 (8) (8)
于是 的后验分布为: 的后验分布为:
 (9) (9)
容易看出,这是倒Gamma分布 ,它就是正态分布 ,它就是正态分布 的后验分布,取其后验分布的期望为 的后验分布,取其后验分布的期望为 的修正后估计,就能得到: 的修正后估计,就能得到:

(二)  的贝叶斯修正 的贝叶斯修正
正态分布的期望 本身也是服从正态分布的, 本身也是服从正态分布的, ,为了方便,我们不妨假设 ,为了方便,我们不妨假设 是已知的,且 是已知的,且 期刊网。由历史数据通过抽样可以得到样本的似然函数为: 期刊网。由历史数据通过抽样可以得到样本的似然函数为:
 (10) (10)
正态分布 的共轭先验分布仍然为正态分布,由此可知 的共轭先验分布仍然为正态分布,由此可知 的共轭先验分布为 的共轭先验分布为 ,且其共轭先验分布的密度函数为: ,且其共轭先验分布的密度函数为:
 (11) (11)
其中 均为已知。 均为已知。
于是 后验分布的密度函数就为: 后验分布的密度函数就为:



显然可以看出 的后验分布是服从正态分布 的后验分布是服从正态分布 ( ( , , ),且其后验分布的期望值为: ),且其后验分布的期望值为:
2/3 首页 上一页 1 2 3 下一页 尾页 |


