| Fig10 Compute results ofmodal shapes of resonant fork system
4 疲劳试验过程的瞬态动力学计算
4.1 系统位移响应的计算
将疲劳试验时的激励力时间历程函数作为边界条件施加到音叉系统有限元模型的相应位置和方向上，输入模态测试得到的1～6阶非刚体模态阻尼比，即可基于有限元模态计算的结果采用模态叠加法进行疲劳试验过程的瞬态动力学计算。
激励力作用在图11中A点的y方向，其形式为 ，其中Fa为激励力幅值，fn为音叉系统1阶固有频率值， 为频率比，t为时间。通过在推杆上安装力传感器，可以测得弯曲疲劳试验时的Fa和值，从而得到激励力时间历程函数。力传感器的安装方法如图12所示。
图11 激励力作用位置
Fig11 The position whereexciting force is applied
   
图12 激励力的测量
Fig12 The measurementmethod of exciting force
测得1015曲轴弯曲疲劳试验中推杆施加的激励力的参数为 。由简化模型理论分析结果可知值不同则音叉系统振动开始阶段的瞬态响应形式有所不同，为了研究实际试验过程中的取值对瞬态响应及疲劳测试结果的影响，考虑取稳态响应幅值相同的一组载荷进行瞬态动力学计算龙源期刊。由式(7)得到简化模型稳态响应幅值的理论解为：
其中 ，l为激励力到摆臂弯曲振动中心的力臂长度。对于确定的试验系统，l、ξ和k均为常数，那么两个值不同的激励力要得到相同的稳态响应幅值，其 值应满足关系式：
 (8)
将音叉系统反向1阶弯曲模态的阻尼比 代入式(8)，可推出 和 两激励力作用下系统的稳态响应幅值与 的激励力作用下系统的稳态响应幅值相同。
分别对3种激励力作用下音叉系统的位移响应进行模态叠加法瞬态动力学计算。取图11中振幅较大的B点，其y向位移响应均为频率等于激励频率、幅值随时间变化的余弦型函数。3种激励力对应的B点y向位移幅值随时间的变化规律如图13所示。
图13 B点y向位移幅值变化规律
Fig13 The displacementamplitudes in axial y of point B against time
当激励力参数为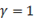 ， 时位移响应幅值随时间单调增大瞬态，但增长速度不断减小，经过20s左右达到稳定值2.738mm。当激励力参数为和 时，接近于1而不等于1，位移幅值出现了剧烈的波动，即图5所示的“拍振”现象。“拍”的周期与频率比有关，频率比越接近于1，“拍”的周期也越大。这与由音叉系统简化模型理论解得到的响应形式是一致的。经过20s左右，“拍振”逐渐衰减消失，位移幅值也达到稳定值2.738mm。
可见在进行1015曲轴弯曲疲劳试验时，由于音叉系统阻尼值较小，激励力引起的自由振动不会很快衰减，在约20s之后系统才达到稳定振动状态。值得注意的是若试验时 ，则在0～20s瞬态响应阶段由于“拍振”会引入一些位移幅值远高于最终稳定值的加载循环。对于的激励力，其在图13中所示的第一个“拍振”周期中的最大位移幅值达到了4.85mm，远高于稳态响应的位移幅值。弯曲疲劳试验的目的是得到20s后稳态循环载荷对应的疲劳寿命，但瞬态响应阶段引入的大载荷循环会对曲轴弯曲疲劳性能产生复杂的影响。大载荷循环的幅值处于一定范围内时，对曲轴起到强化作用，延长了试验寿命；而大载荷循环幅值过高时，会造成较大疲劳损伤甚至引起静强度破坏，极大地缩短试验寿命[8]。这两种情况都降低了疲劳试验结果的准确度。虽然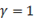时瞬态响应不出现“拍振”现象，不会引入载荷幅值高于稳态响应的瞬态循环，但由图3可知此时系统放大系数太大，载荷将不易控制瞬态，且设备误差的存在也使实际试验中很难调整 值严格为1，因此曲轴弯曲疲劳试验基本都是在值接近于1但不等于1的情况下进行的。那么为了避免瞬态响应阶段大载荷循环对试验结果的影响，不能直接将激励载荷幅值调整到预定值，而应先以幅值很小的激励力激起音叉系统弯曲共振，再逐渐缓慢增加至疲劳试验的预定载荷幅值，继而开始循环计数。
4.2稳态响应下圆角最大应力幅值的计算
通过模态叠加法获得了音叉系统任一点的位移响应之后，可以选择所关心的时间点，对位移解进行模态扩展计算，得到此时刻整个系统的应力分布规律，由此计算曲轴弯曲疲劳试验中无法准确测定的圆角应力幅值。对于试验过程中所测得的激励力 ，B点y向位移在25s～25.06s内
的响应如图14所示。
图14 B点y向位移稳态响应（25s~25.06s内）
Fig14 The steady responseof displacement in axial y of point B (during 25s~25.06s)
此响应接近标准的正弦函数，在25s～25.06s内包含了4个周期，取位移达到最大幅值的任一时刻，例如t=25.034s，进行模态扩展计算，得到此时整个音叉系统的应力分布龙源期刊。摆臂上应力值很小，应力集中位置出现在图15所示的连杆轴颈圆角和主轴颈圆角。对称截面与圆角表面的相交圆弧上的弯曲正应力是弯曲疲劳的决定性参数，根据连杆轴颈圆角和主轴颈圆角形状特点，分别建立其对应的截面极坐标系，如图15所示。其中σM即为圆弧上任一点M的弯曲正应力。t=25.034s时连杆轴颈圆角受压，σM为负值，而主轴颈圆角受拉，σM为正值。由于疲劳试验只关心应力幅值的情况瞬态，因此取 ，其沿各自圆角截面圆弧的分布规律如图16所示。
 
 
3/4 首页 上一页 1 2 3 4 下一页 尾页 |
