谐振式曲轴弯曲疲劳试验系统的动态测试及计算_瞬态

(7)

与大小为M₀的静载荷相比，激励载荷的放大因子为：

(8)

时取最大值瞬态，即达到共振。由于单拐音叉系统,一般认为共振点处。根据式(8)得到共振点附近相对于的变化规律如图3所示。

图3 共振点附近相对于的变化

Fig3 The changes ofagainstnear resonant frequency

可见越接近于1，稳态响应的放大因子越大。当时，载荷放大倍数非常高。因此进行曲轴弯曲疲劳试验时，一般控制激励力角频率w在0.98w_n～1.02w_n的范围内，从而以较小的激励力达到很大的弯曲载荷效果。

当接近1时，对也有影响，越小则越大。另外，由于音叉系统的值很小，激励引起的自由振动衰减很慢，那么在试验开始后较长的一段时间内，系统的受迫响应为自由振动与稳态响应的叠加，并不是弯曲疲劳试验所要求的恒幅简谐振动。根据式(6)可推知若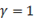，在振动开始阶段的变化规律如图4所示，其为幅值随时间单调增大的正弦函数。

图4 =1时在振动开始阶段的变化

Fig4 The form ofafter vibration startswhen=1

若，在振动开始阶段的变化规律如图5所示，其为幅值随时间振荡变化的正弦型函数，形成了典型的“拍振”。“拍”的周期与激励角频率和系统固有角频率之差有关。由于阻尼的作用，“拍”的幅度随时间逐渐减小。

图5 时在振动开始阶段的变化

Fig5 The formofaftervibration starts when1

2 音叉系统模态测试

采用SIMO法，即单输入多输出法对1015柴油机曲轴的弯曲疲劳试验音叉系统进行模态测试。预计算表明其前6阶模态固有频率在1000Hz以下，因此选用带有尼龙锤帽的力锤激起系统振动龙源期刊。根据音叉的结构特点，在两侧摆臂上设置28个敲击点，编号为N₁~N₂₈，位置如图6所示。各点处力锤敲击方向为N₁~N₆沿y轴正向和x轴正向；N₈~N₁₃沿y轴正向和x轴负向；N₁₅~N₂₀沿y轴负向和x轴正向；N₂₂~N₂₇沿y轴负向和x轴负向；N₇和N₁₄沿y轴正向；N₂₁和N₂₈沿y轴负向。测试时每个测点的采样信号进行10次平均。

图6 敲击点位置

Fig6 The positions ofimpact point

图7 模态测试系统

Fig7 The modal testsystem

使用14个加速度传感器采集振动信号瞬态，分别安装在摆臂外表面N₂、N₄、N₆、N₇、N₈、N₁₀、N₁₂、N₁₆、N₁₈、N₂₀、N₂₁、N₂₂、N₂₄、N₂₆处。采样带宽选1280Hz，谱线为4096，采样频率为0.3125Hz。整个测试系统如图7所示。

采用Polymax法对综合传递函数进行模态参数识别，得到试件音叉系统1~6阶非刚体模态参数如表1所示，振型如图8(1)～8(6)所示，虚线表示未变形的形状。

表1 试件音叉系统1~6阶模态参数测试结果

Tab1 Modal test resultsof the resonant fork system

图8 试件音叉系统1~6阶振型测试结果

Fig8 Test results ofmodal shapes of resonant fork system

第1阶模态振型为曲轴弯曲疲劳试验所要求的反向一阶弯曲，其频率为66.96Hz。疲劳试验时激励频率应控制在此值附近，以实现谐振弯曲加载。第2阶模态振型为同向一阶扭转，其频率值与第1阶频率相差较大，则进行弯曲疲劳试验时其它阶模态对音叉系统整体振动的影响远小于第1阶模态，从而保证曲轴单拐基本承受纯弯曲载荷。

3 音叉系统有限元模态分析

建立1015柴油机曲轴弯曲疲劳试验音叉系统的几何模型时，由于锥套连接装置和曲拐油孔对系统整体的质量分布几乎没有影响，其存在与否不会降低有限元模态分析的准确度，因此将这些局部特征省略以减小计算规模。根据模型的对称性，首先对由对称截面切开的1/4曲轴单拐进行六面体网格划分，考虑到后续瞬态动力学分析的需要，在弯曲应力较大的曲轴圆角区域采用了较高的单元密度，如图9(a)所示。然后基于1/4曲轴单拐有限元模型对其相应一侧的1/2摆臂进行六面体网格划分，得到由对称截面切开的1/4音叉系统的有限元模型，经过两次对称映射处理后得到整个试件音叉系统的有限元模型，如图9(b)所示。

图9 音叉系统有限元模型

Fig9 Finite element modelof resonant fork system

试验过程中音叉系统使用钢丝绳悬挂在支架上，因此对其进行自由模态分析，得到1～6阶非刚体模态参数如表2所示瞬态，振型如图10(1)～10(6)所示。

1～6阶非刚体模态振型的计算结果与测试结果一致，固有频率计算值与测试值也较为接近，特别是弯曲疲劳试验所利用的第1阶模态，固有频率值的差别在2％以内，因此有限元计算结果是足够精确的。

表2 试件音叉系统1~6阶模态计算结果

Tab2 Modal computeresults of resonant fork system

图10 试件音叉系统1~6阶振型计算结果

 2/4   首页 上一页 1 2 3 4 下一页 尾页