| 此时按方案2铺设管线总费用最省。
③当 ,即 ,即 时, 时,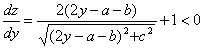 ,所以z在y ,所以z在y 上为减函数,故当y=a时,z取得最小值 上为减函数,故当y=a时,z取得最小值 。因此可得方案4:如图4,将车站建在坐标原点,铺设共用管线OA及非共用管线AB。此时铺设管线总长度最小为 。因此可得方案4:如图4,将车站建在坐标原点,铺设共用管线OA及非共用管线AB。此时铺设管线总长度最小为 ,即铺设管线总费用最省。 ,即铺设管线总费用最省。
共用管线单位费用与非共用管线单位费用相同时
共用管线单位费用与非共用管线单位费用不同时
综上可得,针对a、b、c不同关系下的各种情形,得管线铺设的最佳方案如下:
|
a、b、c的关系
|

|

|

|

|
|
最佳方案选 择
|
方案4
|
方案3
|
方案2
|
方案1
|
|
最低费 用W
|

|

|

|

|
(3)若铺设共用管线且共用管线单位费用与非共用管线单位费用不同
设共用管线单位费用为非共用管线单位费用的 倍,即 倍,即 = = 。 。
运用(2)所用方法同理可得各种情形下管线铺设的最佳方案:求得
 , , ,E( ,E( ,0),Q( ,0),Q( , , ) )
|
C的取值
|

|

|

|

|
|
方案选择
|
方案4
|
方案3
|
方案2
|
方案1
|
|
最低费用W
|

|
 
|

|

|
5.2问题2模型的建立与求解
5.2.1对各因素权重的确定
通过引入两个因素对附加费用影响的程度大小的比值得到成对比较矩阵如下:

其中 =2即表示公司一和公司二对附加费用的影响之比为2:1; =2即表示公司一和公司二对附加费用的影响之比为2:1; =1即表示公司二和公司三对附加费用的影响之比为1:1。求出对比矩阵 =1即表示公司二和公司三对附加费用的影响之比为1:1。求出对比矩阵 的最大特征根为 的最大特征根为 ,对应的特征向量归一后为 ,对应的特征向量归一后为

即3种因素在弊端指数中所占的权重,由此我们可以得到
所以附加费用为:
5.2.2模型建立与求解
 
图6图7
设点   ,则铺设管线的总长度为(如图6): ,则铺设管线的总长度为(如图6):

建立目标函数:Min 
约束条件:  
输入lingo2(见附录)程序得到: 万元 万元 (如图7)。 (如图7)。
5.3问题3的模型建立与求解
5.3.1模型建立
如图6所示,建立目标函数:
Min 约束条件: 约束条件: 0 0 
输入lingo4(见附录)程序得: 万元 万元  
(如下图)。

6模型评价
6.1模型的优点:
1模型原理简单明了,容易理解
2运用lingo程序进行计算,是计算结果更加准确。
3模型原理简单明了,容易理解
6.2模型缺点:对问题一考虑情形不完全。 2/2 首页 上一页 1 2 |


