对于任意函数x(t),定义 , ,
令 , ,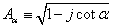 ,则分数阶域卷积的定义式可表达为: ,则分数阶域卷积的定义式可表达为:
 其中 其中 代表p阶分数阶域卷积。 代表p阶分数阶域卷积。
设 的p阶分数阶傅里叶变换分别为 的p阶分数阶傅里叶变换分别为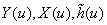 ,那么根据分数阶傅里叶变换的性质,分数阶卷积在变换域中可表示为 ,那么根据分数阶傅里叶变换的性质,分数阶卷积在变换域中可表示为 。 。
即分数阶卷积定理可表述为 (7) (7)
在图1中判决反馈均衡器,信号 再通过均衡器 再通过均衡器 ,可得到 ,可得到
那么在不考虑噪声的情况下,为完全消除码间干扰,根据迫零准则,应该有 ,由(7)式可知,均衡器 ,由(7)式可知,均衡器 的分数阶傅里叶变换 的分数阶傅里叶变换 满足 满足 。即 。即  (8) (8)
2。3最优阶次p的选择
对于分数阶时变信道 ,与频域最小二乘信道估计类似,可通过变换域最小二乘信道估计方法估计出信道 ,与频域最小二乘信道估计类似,可通过变换域最小二乘信道估计方法估计出信道 的分数阶傅里叶变换 的分数阶傅里叶变换 。具体过程是在图1中(暂不考虑噪声),发送训练序列 。具体过程是在图1中(暂不考虑噪声),发送训练序列 ,在接收端可得到接收训练序列 ,在接收端可得到接收训练序列 。令 。令 分别为 分别为 , , 的分数阶傅里叶变换。这样可得到相应FRFT域响应 的分数阶傅里叶变换。这样可得到相应FRFT域响应 的估计值 的估计值 。记号 。记号 代表 代表 。在存在噪声 。在存在噪声 的情况下,由变换域的迫零准则可得到线性均衡器的误差函数 的情况下,由变换域的迫零准则可得到线性均衡器的误差函数 。其中 。其中 是噪声 是噪声 的p阶分数阶傅里叶变换。则均方误差 的p阶分数阶傅里叶变换。则均方误差 可表示为 可表示为 其中 其中 是frft域的噪声方差,它与时域的噪声方差相等。这样可得到以下结论,当信噪比不变, 是frft域的噪声方差,它与时域的噪声方差相等。这样可得到以下结论,当信噪比不变, 的模恒为1时,可得到均衡器 的模恒为1时,可得到均衡器 的最小值。当 的最小值。当 衰落深度较大时,会使该频点噪声增大, 衰落深度较大时,会使该频点噪声增大, 也相应增大。因此,为获得最优的均衡效果,应尽量选择使 也相应增大。因此,为获得最优的均衡效果,应尽量选择使 与1的方差能取最小值的阶次p进行均衡。 与1的方差能取最小值的阶次p进行均衡。
目标函数自然可定义为 ,因而,使 ,因而,使 取最小值的阶次p就是均衡器的最优阶次。它可定义为 取最小值的阶次p就是均衡器的最优阶次。它可定义为 。当 。当 正好为1时,最优阶次 正好为1时,最优阶次 对应的变换域均衡就是频域均衡。 对应的变换域均衡就是频域均衡。
3.均衡系统的实现
图 2为采用MLSE (最大似然序列均衡器)的通信系统模型,它包括调制器,ISI+白噪声信道模型和解调器等几个部分。其中调制器包括卷积编码器,MPSK调制器。解调器包括MPSK解调器,均衡器及viterbi译码器。 在解调器中,可以采用自适应判决反馈均衡器和快速收敛的平方根卡尔曼自适应算法来消除ISI并实时跟踪信道的变化。同时,为了有效地控制由残留 ISI 和白噪声干扰产生的差错,采用了卷积码与MPSK调制相结合的网格编码调制(TCM)技术,在接收端作软判决和最大似然译码.信源产生的信息序列a(k)经卷积编码及MPSK调制(即TCM编码)后产生信号序列b(k),经ISI信道传播,到达接收端的信号r1(k)已经受到了ISI和白噪声干扰,解调器对其进行MPSK解调,得到r(k),并对其进行判决反馈均衡消除干扰,产生a(k)的估值序列A(k)。
 图2 MLSE均衡器结构框图 图2 MLSE均衡器结构框图
图2中,判决反馈均衡器的具体结构如图3所示。该均衡器由前向滤波器(FFF)和反馈滤波器(FBF)组成。其中前向滤波器(FFF)由变换域线性均衡器代替,它的输入来自8PSK解调后的输出r(k)。而FFF在变换域进行操作,即先对r(k)进行串并变换,再将信号流按帧进行分数阶傅里叶变换,再对每帧作变换域线性均衡。均衡后作分数阶傅里叶反变换,返回时域,最后串行输出z(k)。
(Ⅰ).FFF具体工作过程如下:
(1)在接收机中,对下变频后的基带数据进行训练序列与数据序列分离。
(2)将发送的训练序列及接收的训练序列在不同阶次的变换域中进行最小二乘信道估计,根据目标函数 来选择最优阶次 来选择最优阶次 。 。
(3) 得到最优阶次 后,由(8)式 后,由(8)式 来确定最优阶次下的变换域均衡的乘性抽头系数 来确定最优阶次下的变换域均衡的乘性抽头系数 。 。
(4)将数据帧进行串并变换并进行分块处理,即将数据分成一定长度的数据块,对每一数据块利用FRFT快速算法变换到 对应的变换域。 对应的变换域。
(5)将变换结果通过乘性滤波器 进行变换域的线性均衡,再进行FRFT的逆变换IFRFT返回时域,之后还需将每一数据块重复进行以上操作,得到线性均衡后的时域数据z(k)。 进行变换域的线性均衡,再进行FRFT的逆变换IFRFT返回时域,之后还需将每一数据块重复进行以上操作,得到线性均衡后的时域数据z(k)。
 图3 MLSE均衡器的具体结构 图3 MLSE均衡器的具体结构
(Ⅱ).判决反馈过程:
为了进一步抑制当前时刻之前的信息符号所产生的ISI,在线性均衡之后还需引入判决反馈均衡器FBF。
当判决单元采用直接判决时, 被认为是序列 被认为是序列 的估值序列,判决误差为 的估值序列,判决误差为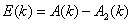 。 。 时刻的判决均方误差就是 时刻的判决均方误差就是 。而最小均方算法(LMS)所用的准则是使均衡器的期望输出值 。而最小均方算法(LMS)所用的准则是使均衡器的期望输出值 (判决值)与实际输出值 (判决值)与实际输出值 之间的均方误差 之间的均方误差 最小化的原则。在实际应用中判决反馈均衡器,均方误差的最小值是按照一种随机梯度算法通过递归求出的。最小均方算法是一种简单的均衡算法,设FBF用 最小化的原则。在实际应用中判决反馈均衡器,均方误差的最小值是按照一种随机梯度算法通过递归求出的。最小均方算法是一种简单的均衡算法,设FBF用 表示,则FBF的输出表示为 表示,则FBF的输出表示为 (9) (9)
2/3 首页 上一页 1 2 3 下一页 尾页 |


