| 考虑在一个库存周期中,零售商没有选择紧急订购策略的期望成本:
 (2) (2)
零售商在阶段b中选择紧急订购策略的期望成本:
 (3) (3)

其中: 满足 满足 ,即紧急订购提前期越短,订购成本越高。 ,即紧急订购提前期越短,订购成本越高。
令:  (4) (4)
即:在阶段b库存量 时,零售商选择紧急订购,订购量为 时,零售商选择紧急订购,订购量为 ;反之选择正常订购。下面我们对(3)式求偏导: ;反之选择正常订购。下面我们对(3)式求偏导:


可知F(x)为单增函数,如果K(l)增加,  y都有 y都有 增加,因此 增加,因此 增加,由定义知 增加,由定义知 必然下降。 必然下降。
如果Q是常数,紧急订购策略下的订购点 必然小于等于(Q,R)中的 必然小于等于(Q,R)中的 ,因为在紧急订购策略中,持有成本和缺货成本(H,B)等于(Q,R)模型中的相应成本。由于K>A,则紧急订购降低了缺货成本,为了使缺货概率达到最优水平,必然 ,因为在紧急订购策略中,持有成本和缺货成本(H,B)等于(Q,R)模型中的相应成本。由于K>A,则紧急订购降低了缺货成本,为了使缺货概率达到最优水平,必然 。 。
3 仿真优化
对于随机性库存系统,因为变量的随机性以及系统变量之间存在的复杂非线性关系,用解析方法求解不但需要作一些假设,而且公式复杂求解困难。启发式算法则不受随机变量的影响,而且可以更自然地描述系统变量之间的非线性关系。因此本文采用遗传算法计算复合(Q,R)模型最优解。
3.1 遗传算法
遗传算法是一种全局优化自适应概率搜索的仿生算法,它借鉴生物的自然选择和遗传进化进制,使用群体搜索技术,通过对当前群体施加选择、交叉、变异等一系列遗传操作,从而产生出新一代的群体,并逐步使群体进化到包含或接近最优解的状态。仿真算法的优化步骤如下:
(1)针对复合(Q,R)库存模型的特点,采用实数队作为编码,将 作为库存模型仿真优化的染色体; 作为库存模型仿真优化的染色体;
(2)根据编码方案产生初始种群;
(3)在遗传算法终止前循环执行(4)—(6);
(4)计算适应度函数值: ,将个体的适应度由大到小进行排序; ,将个体的适应度由大到小进行排序;
(5)选择算子:采用最优保存策略,具体操作过程是:
(a)找出当前群体中适应度最高的个体和适应度最低的个体;
(b)若当前群体中最佳个体的适应度比总的迄今为止的最好个体的适应度还要高,则以当前群体中的最佳个体作为新的迄今为止的最好个体。
(6)交叉算子:在相互配对的两个个体编码串中随机设置两个交叉点,交换两个个体在所设定的两个交叉点之间的部分染色体;
(7)变异算子:均匀变异,具体操作过程是:
(a)依次指定个体编码串中的每个基因座为变异点;
(b)对每一个变异点,以变异概率 从对应基因的取值范围内取一随机数来替代原有的基因值。 从对应基因的取值范围内取一随机数来替代原有的基因值。
4 案例分析
由RFID跟踪的销售记录本科毕业论文格式,某卷烟商业企业品名为红河(软甲)某月份日销售记录如表1所示,提前期分布如表二所示:
表一 某月份红河(软甲)日销售记录
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
………
|
|
127
|
115
|
78
|
136
|
91
|
102
|
109
|
75
|
86
|
………
|
表二 提前期分布
|
提前期/天
|
2
|
3
|
4
|
|
概率(%)
|
65
|
30
|
5
|
通过RFID跟踪获得的数据可以及时、准确地得到所需参数:
日需求均值: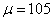 日需求标准差: 日需求标准差:
持有成本:H=4400缺货成本:B=530
正常订购成本:A=120 紧急订购成本:K=[130,220]
紧急订购提前期: =2天 =2天
现将正常订购提前期分为三个阶段b=1,2,3, ,Q=[400,700],R=[250,450] ,Q=[400,700],R=[250,450]
由前述遗传算法可得到传统的(Q,R)模型中的最优解Q=486;R=372;K=130; =0.85,在服务水平为95%时可节约成本为4.4%,降低缺货成本81.2%,如下表三: =0.85,在服务水平为95%时可节约成本为4.4%,降低缺货成本81.2%,如下表三:
表三 传统(Q,R)模型与复合(Q,R)模型比较结果
|
K
|
130
|
145
|
160
|
175
|
190
|
205
|
220
|
|

|
0.85
|
0.9
|
0.75
|
0.6
|
0.5
|
0.4
|
0.3
|
|

|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
Q
|
486
|
486
|
486
|
486
|
486
|
486
|
486
|
|
R
|
372
|
372
|
372
|
372
|
372
|
372
|
372
|
|

|
6325
|
6325
|
6325
|
6325
|
6325
|
6325
|
6325
|
|

|
417
|
417
|
417
|
417
|
417
|
417
|
417
|
|

|
6044
|
6056
|
6087
|
6121
|
6154
|
6103
|
6093
|
|

|
78
|
83
|
87
|
84
|
95
|
90
|
87
|
|

|
4.4%
|
4.2%
|
3.8%
|
3.2%
|
2.7%
|
3.5%
|
3.7%
|
|

|
81.2%
|
80.1%
|
79.1%
|
79.8%
|
77.2%
|
78.4%
|
79.1%
|
以一个周期内的库存成本作为目标函数,采用遗传算法的寻优过程(通过MATLAB7.0编程实现)如图3所示:

图3 遗传算法寻优迭代过程
(Q,R)模型中当库存位置到达订购点R=372时,则订购批量Q=486,为了尽可能的避免缺货的发生,当库存位置到达Yb=315时,则采用复合(Q,R)模型中的紧急订购策略,订购批量为aQ=413,传统的(Q,R)模型与复合(Q,R)模型的比较如图4所示:

图4 传统(Q,R)模型与复合(Q,R)模型
4 结语
本文利用RFID信息采集的实时性、准确性,在传统的(Q,R)库存控制模型的基础上定义了复合的(Q,R)模型,由于模型的非线性给模型的精确求解带来了困难,本文采用启发式算法中的遗传算法寻优求解,并结合红河香烟的库存管理实际案例分析比较了传统的(Q,R)模型与复合模型,采用复合模型可以降低库存成本3%—4%,降低缺货成本78%—81%,可见复合的(Q,R)库存控制模型具有更明显的经济效益。
由于RFID读取率还不能达到100%,从而难免会有数据缺失,因此在数据缺失的情况下库存控制模型需要做怎样的改动本文没有作进一步的探索。
参考文献:
[1]郭龙岩,李泉林,王璞.基于RFID的供应链的信息与成本结构[J],中国电子商情,2006,(2):58-64
[2]Nath B,Reynolds F, Want R. RFID Technology and Applications[J]. IEEE PervasiveComputing, 2009, 5(1):22-24
[3]Delong B.How the US Military is Achieving Total Asset Visibility and More Using RFID andMEMS[R]. Invited Presentation, Smart LABELS USA, Cambridge, MA, 2003.
[4]Abell P.Item Tracking: Myths and Realities[J]. RFID Journal,2003,12(2):219-232.
[5]Romanow K, S Lundstrom. RFID in 2005: The What is More ImportantThan the When with Wal-Mart Edict [J]. AMR Research, 2003, 8(2):9-22
[6]杜玉兰,赵磊.烟草企业决策支持系统模型的研究[J],广西轻工业,2007,59(9):59-61
[7]裴峰,林国龙,杨权斌.RFID技术与现代物流信息系统设计[J],上海大学学报,2005,26(4):52-56.
[8]Brewer A, Sloan N,Landers TL. Intelligent tracking inmanufacturing[J]. J Intell Manuf ,1999,10:245–250
[9]Moran HJ, McFarlane D, Milne TP.Use case approach fordetermining the impact of Auto-ID implementations on business informationsystems[J]. MIT Auto-ID Center White Paper ,2008
[10]Garcia A, McFarlane D, Fletcher M, Thorne A. Auto-ID inmaterials handling[J].MIT Auto-ID CenterWhite Paper,2008
2/2 首页 上一页 1 2 |


