论文导读::复合实物期权定价模型能更贴切地反映在3G项目中的多重期权特性。
论文关键词:复合实物期权,3G投资,项目投资价值
一、事件及背景分析
中国已经逐渐进入广泛使用第三代移动通信技术(俗称3G)的时代,但对电信运营商而言,3G网络的建设和运营具有规模大、分阶段、周期长和未来不确定性较高等特点。如何评估3G项目的投资价值一直是广为关注的焦点。传统的项目投资价值分析方法不能满足对不确定性较高的项目进行定价的要求。复合实物期权定价模型能更贴切地反映在3G项目中的多重期权特性,更适合对阶段性较强的项目进行价值分析。本文将运用复合实物期权模型对澳门基于CDMA技术的3G项目进行定价分析。
澳门3G项目(CDMA技术标准)的建设具有明显的阶段性,其投资历程如下:
表1-1 澳门CDMA投资历程
|
时间
|
事件
|
意义
|
投资计划
|
|
2005年3月10日
|
中国联通中标获得澳门CDMA牌照
|
正式进入澳门移动通信市场
|
-
|
|
2005年5月27日
|
中国联通获准经营采用CDMA2000 1X系统的公共地面流动通信电信网络及提供跨地域流动电信服务,有效期为8年。
|
中国联通获准提供CDMA漫游服务的权利
|
首年投资1.71亿澳门元,建成CDMA 1X制式网络,以提供漫游服务
|
|
2005年10月18日
|
CDMA澳门流动电信网络开通
|
开始提供CDMA漫游服务
|
-
|
|
2006年8月10日
|
中国联通获准经营采用CDMA2000 1X系统的公共地面流动通信电信网络及提供两个频段内运作的公用地面流动电信服务
|
中国联通获得本地运营CDMA服务牌照。CDMA2000 1X可平滑升级到3G网路。
|
2006年计划增加投资4800万澳门元,在后续二年内累计投资额不低于4000万元
|
|
2007年5月29日
|
中国联通获正式建立及运营3G的牌照
|
建立及运营CDMA2000 1X EV-DO系统,真正提供3G服务
|
为建立3G业务,首年将投资4000万澳门元;随后三年累计投资超过9000万澳门元
|
|
2008年7月27日
|
中国联通将包括中国联通(澳门)有限公司100%股权在内的CDMA业务转让予中国电信
|
澳门CDMA业务运营的主体变更为中国电信
|
已发放的CDMA 3G牌照继续生效,仅变更牌照人名称,投资规模及计划没有变化
|
资料来源:部分来自澳门印务局《第173/2007号行政长官批示》项目投资价值,《第235/2006号行政长官批示》,《第185/2005号行政长官批示》
组成澳门CDMA项目的建设的三个阶段具有非常明显的复合期权特性。在第一期投资启动以后,投资决策者(运营商)会有选择进行第二阶段和第三阶段两个相互关联的投资的权利或机会,而继续进行投资这一决定是基于对一段时期后澳门3G市场的发展情况和澳门CDMA的网络建设情况及其市场竞争力等的判断。在适当的时机(譬如3G牌照已经发放等情况下),当项目的价值超过临界值,该投资才会被启动,所以启动第二期投资和第三期投资的权利是看涨期权。
具体来看,第三期投资启动的临界条件是进行3G网络扩容后(第三期投资)所带来的整个项目的现金流入量净增量的现值大于第三期的投资额,此时理性的投资决策者会选择执行期权,继续投资。第二期投资启动的临界条件是进行3G网络升级后(第二期投资)所带来的整个项目的现金流入量净增量的现值,加上由第二期投资所获得的第三期投资的期权价值,大于第二期投资的投资额,此时理性的投资决策者会选择执行期权,继续投资。所以,对第二、三阶段的价值可以用复合期权的方法进行分析。
尽管在2008年7月27日,在国内电信业大重组的背景下,中国联通将澳门CDMA业务转让予另一运营商——中国电信,但项目的运营团队、资金投入计划(澳门发放3G牌照所要求)、已有的建设水平和网络基础等都没有发生变化,因此可以认为这种整体转让并不影响我们对澳门地区CDMA项目经营运营的价值分析论文开题报告。
本文将站在2005年运营商(当时是中国联通)还未大规模进入但正在计划进入澳门移动通信市场的时点上,将澳门进行的CDMA网络投资(包括2G,3G以及未来4G的投资运营)作为一个项目,用复合实物期权模型对整个战略投资项目进行定价。
二、模型化分析及参数估计
1、模型设定:多阶段投资模型及其假设
Geske 于1979年给出了简单复合期权(复合期数n=2)定价的一般公式,根据Geske模型的思路,我们结合多阶段投资的特点,对模型的参数赋予新的意义,提出多阶段投资模型及其假设如下:
① 投资的期数有三期(每期的投资分别为 项目投资价值, 项目投资价值, 和 和 ),涉及三个时点(0,t和T),如下图所示: ),涉及三个时点(0,t和T),如下图所示:
 
图2-1 投资期分布
② 每期投资都产生独立的现金流,后续的投资不会改变前期投资的现金流量。后续投资所带来的独立现金流量可以看作是该投资带来的项目现金流的净增量。
③ 后续投资以前期投资为基础。在0时刻进行投资,获得在t和T进行投资的机会;在t时刻进行投资,获得在T进行投资的机会。如果没有前期投资,后续投资不会出现。
④ 在初始投资启动后,投资者只能在t时刻与T时刻选择是否继续进行投资,这种选择权利不会在到期前被行使,即假设这是欧式期权。
⑤ 假设市场无套利机会存在而且投资者风险中性。
⑥ 价值贴现时使用连续复利。
(3)多阶段投资模型的求解
Baldwin和Trigeorgis提出,考虑了管理灵活性(期权价值)后的项目净现值公式变为:扩展后的净现值=传统的净现值+管理灵活性的价值
即:ENPV=TNPV+ 公式(1) 公式(1)
在本模型中,ENPV是考虑了项目期权价值后的净现值,TNPV是第一期投资的净现值;将后两期投资看作是两个相互关联的期权,即为一个复合期权,标的期权的到期时间是T,混合期权的到期时间是t;该复合期权是买权的买权,其价值为 。 。
 的求解公式可以应用Geske公式中买权的买权公式变形得到: 的求解公式可以应用Geske公式中买权的买权公式变形得到:
 公式(2) 公式(2)
其中, ,公式(3) ,公式(3)
 ,公式(4) ,公式(4)
 ,公式(5) ,公式(5)
 公式(6) 公式(6)
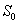 为第三期投资引起的现金流入量在0时刻的现值; 为第三期投资引起的现金流入量在0时刻的现值;
 为第三期投资引起的现金流入量在T时刻的现值; 为第三期投资引起的现金流入量在T时刻的现值;
 为在t时刻,第二期里现金流出量减去现金流入量的差,即 为在t时刻,第二期里现金流出量减去现金流入量的差,即 与第二期现金流入量的现值的差; 与第二期现金流入量的现值的差;
k为第三期投资的现金流出量在T时刻的现值,即 ; ;
 为第三期投资项目价值的波动率; 为第三期投资项目价值的波动率;
 为无风险利率; 为无风险利率;
 为一元标准正态累积分布函数; 为一元标准正态累积分布函数;
 为二元标准正态累积分布函数 为二元标准正态累积分布函数
 为混合期权得以执行的临界值,即第二期投资 为混合期权得以执行的临界值,即第二期投资 得以启动的临界值(这里的 得以启动的临界值(这里的 相当于Geske公式中的X 相当于Geske公式中的X )项目投资价值,通过以下公式求解: )项目投资价值,通过以下公式求解:
 ,公式(7) ,公式(7)
其中, 公式(8) 公式(8)
2、模型假设
(1)假设项目的投资期为从2005年至2015年共10年。
1/3 1 2 3 下一页 尾页 |


