 (2) (2)
 (3) (3)
式中E表示光子的能量,这意味着,尽管1-和1的差值很小 ,但当使用光子能量非常高、波长很短的X射线作光源时,即使是不太大的厚度或密度变化,也可能产生相当大的位相漂移,这为相衬成像提供了可能。
2.2 同轴相衬成像基本原理
2.2.1 相衬成像基本原理
相衬法成像是由德国科学家泽尼克在1935年发明的一种成像方法[25],它能够把位相物体转换成强度分布。
具体做法为在一块玻璃基片的中心滴上一滴小液滴,设液滴的光学厚度为nh,从而引起零级相移 ,这就制成了一块相位板(图4),将它放在显微镜的后焦面上,当作滤波器使用。 ,这就制成了一块相位板(图4),将它放在显微镜的后焦面上,当作滤波器使用。
设样品的透过率函数为:
 (4) (4)
不加相位板时机电一体化论文,在正入射的相干光照射下,物平面的复振幅分布为: (5) (5)
式中 包含振幅A和位相 包含振幅A和位相 两部分, 两部分, 为入射光的振幅。式子右边第一项是直流成分,代表沿光轴传播的平面衍射波,它在傅氏面上时集中于焦点的0级衍射斑,式中的级数中其它各项代表复杂的波前,他们的频谱弥漫在傅氏面上各处。 为入射光的振幅。式子右边第一项是直流成分,代表沿光轴传播的平面衍射波,它在傅氏面上时集中于焦点的0级衍射斑,式中的级数中其它各项代表复杂的波前,他们的频谱弥漫在傅氏面上各处。
加入相位板后,傅氏面上的0级斑相移,同时假设它有一定的透过率a,而它的频谱成分改变不大,可以忽略,则复振幅的分布为:
 (6) (6)
于是像面上的光强分布为:
(7)
这时像面上就不再是一片均匀强度了,出现了与物的相位信息相关的黑白图像,在a=1,的情况下, , , ,则: ,则:
 (8) (8)
从上式可知,像面上的强度分布与样品的相位信息成线性关系,即样品的相位分布调制了像面上的光强分布,式中的线性系数 反映了调制的程度,这就是相衬的基本成像原理。 反映了调制的程度,这就是相衬的基本成像原理。
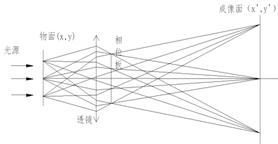
图4 相衬成像原理
2.2.2 同轴相衬成像
该技术问世至今,已经发展出了四种相位衬度成像方法,分别为:通过干涉条纹移动探测样品引起的相位改变的干涉成像法;利用晶体对入射光的角度选择性,探测样品引起的折射角的衍射增强成像法;利用光栅剪切干涉获得对样品折射光的角度选择性,探测样品引起的折射角的光栅剪切相位衬度成像法;样品产生的波阵面弯曲经过一定距离d的自由传播,转变为光的聚焦与发散,相位二阶导数转变为光强的二阶导数,形成样品的像的同轴相位衬度成像法[26]。
在各种相衬成像技术中,同轴相衬成像技术具有光路简单、视场大以及图像中无伪像等优点,该方法不需要特别的样品准备和复杂的光学器件,样品在成像过程中也不会受到光学元件运行不正常等因素的干扰。其成像及工作原理如下[25~29]:
假定一薄层物体位于z = 0平面上,被沿z方向传播的单色平面波exp (-ikz) 照明(图5),物体的透射函数可写成:
(9)
式中: 表示吸收的变化, 表示吸收的变化, 表示位相的变化, 表示位相的变化, 为线性吸收系数, 为线性吸收系数, 为折射率的实部。 为折射率的实部。
对于弱吸收和弱位相的物体,可以近似成:
 (10) (10)
在z > 0的连续平面里,若物体尺寸与波长 相比很大,作傍轴条件近似,根据菲涅耳衍射理论,波函数的振幅可以用 Fresnel-Kirchhoff 积分形式写出: 相比很大,作傍轴条件近似,根据菲涅耳衍射理论,波函数的振幅可以用 Fresnel-Kirchhoff 积分形式写出:
 (11) (11)
式中 和 和 分别是像平面和物平面坐标,两者距离为z。根据菲涅耳衍射公式,可以定义一个权重函数: 分别是像平面和物平面坐标,两者距离为z。根据菲涅耳衍射公式,可以定义一个权重函数:
 (12) (12)
于是(11) 式可以写成卷积形式:
 (13) (13)
(13)式表明像平面上的衍射场的复振幅是物场的复振幅与菲涅耳传播函数的卷积。经过一系列的傅立叶变化运算,得到:
 (14) (14)
式中第一项 表示透射项,第二项 表示透射项,第二项 表示吸收成像衬度,第三项 表示吸收成像衬度,第三项 表示位相的成像衬度,函数 表示位相的成像衬度,函数 和 和 分别是振幅强度和位相强度的衬度传递函数(CTF)。 分别是振幅强度和位相强度的衬度传递函数(CTF)。
对于弱的纯吸收和纯位相物体 , , ;对于足够小的 ;对于足够小的 , , 则: 则:
 (15) (15)

图5 X射线同轴相衬成像原理
根据二阶拉普拉斯算子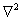 二维傅立叶变化性质: 二维傅立叶变化性质:
 (16) (16)
式中, 是 是 的二维傅立叶变化,则可得到在z平面(成像平面)上振幅分布和强度分布为: 的二维傅立叶变化,则可得到在z平面(成像平面)上振幅分布和强度分布为:
 (17) (17)
 (18) (18)
对于X射线而言, ,经过进一步简化,可以得到: ,经过进一步简化,可以得到:
2/3 首页 上一页 1 2 3 下一页 尾页 |


