（5）把调整后 对应行与 对应列的交叉方格划掉，表示设备与设备的相邻位置不可更改。然后再转入（1）,重新计算末划掉方格的 ，如此反复，直至所有末划掉的方格中均为0,便得到最优解。
3.3 计算与优化
图2为某生产系统设备排布及物料流动关系图，设备布局成2行6列免费论文下载。设第1列和第2列间距为2.5米，第2列和第3列间距为5米最大元素法，第3列和第4列间距为7.5米，第4列和第5列间距为10米，第5列和第6列间距为12.5米；第1行和第2行间距为5米；入口到第1列设备间距为5米，出口到第6列设备间距为5米。由于行车轨道限制，行车只能走直角，如M1与M8之间距离为7.5米，M3与M11之间距离为22.5米。设处于奇（偶）列位置的设备之间物料单位移动费用为1 百元；奇偶列位置的设备之间物料单位移动费用为2 百元,各设备到入口、出口的物料单位移动费用为2 百元。
图3 第一次调整后车间设备排布及物料流动关系图
图2所示车间设备排布混乱，费用较大。运用最大元素法优化车间设备布置，具体步骤如下：
第一步：计算图2所有设备之间的 填入表1对角线以下区域对应方格中，由表1可知最大元素法， 为所有最大值，因此优先互换M2和M8，得图3。
第二步：划掉M1和M8、M7和M2所对应的方格。
表1 设备布置优化过程1（图2、图3）中的△Cxy值
（△Cxy表示Mx与My互换位置后物流费用的减少值，单位为(百元)；x和y均为设备标号）
|
|
M1
|
M2
|
M3
|
M4
|
M5
|
M6
|
M7
|
M8
|
M9
|
M10
|
M11
|
M12
|
|
M1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
|
M2
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
|
M3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
M4
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
0
|
|
0
|
|
M5
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
|
M6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
M7
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
M8
|
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M9
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
|
M10
|
0
|
0
|
0
|
0
|
|
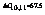
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M11
|
0
|
0
|
|
|
0
|
|
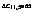
0
|
0
|
0
|
0
|
0
|
0
|
|
M12
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
第三步：计算图3所有设备之间的填入表1对角线以上区域对应方格中，由表1可知， 为所有最大值，因此优先互换M10和M11，得图4。
第四步：划掉M4和M11所对应的方格免费论文下载。
图4 第二次调整后车间设备排布及物料流动关系图
第五步：计算图4所有设备之间的填入表2对角线以下区域对应方格中，由表2可知， 为所有最大值最大元素法，因此优先互换M6和M12，得图5。
第六步：划掉M5和M12所对应的方格。
图5 第三次调整后车间设备排布及物料流动关系图
表2 设备布置优化过程2（图3、图4）中的△Cxy值
|
|
M1
|
M2
|
M3
|
M4
|
M5
|
M6
|
M7
|
M8
|
M9
|
M10
|
M11
|
M12
|
|
M1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
|
M2
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
|
M3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
M4
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
0
|
|
M5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
|
|
M6
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
|
M7
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M8
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M9
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M10
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M11
|
0
|
0
|
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
M12
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
第七步：计算图5所有设备之间的填入表2对角线以上区域对应方格中，由表2可知，为所有最大值，因此优先互换M3和M19，得图6。
第八步：划掉M3和M11所对应的方格。
图6 第四次调整后车间设备排布及物料流动关系图
第九步：计算图6所有设备之间的填入表3对角线以下区域对应方格中，划掉方格不予考虑，经计算图6中所有未划掉方格中值均为零，因此，图6为设备最优布置图。
4 成本节约分析
通过上述方法的优化，对比优化前后的费用如表4所示。
表4 优化前后物流费用比较（单位：距离为米，费用为吨百元）
|
优化前
|
优化后
|
|
①10吨单位移动费用为1 百元的距离：
②10吨单位移动费用为2百元的距离：
③费用：
|
①10吨单位移动费用为1 百元的距离：
②10吨单位移动费用为2百元的距离：
③费用：
|
|
④15吨单位移动费用为1 百元的距离：
⑤15吨单位移动费用为2百元的距离：
⑥费用：
|
④15吨单位移动费用为1 百元的距离：
⑤15吨单位移动费用为2百元的距离：
⑥费用：
|
|
⑦总费用：
|
⑦总费用：
|
|
⑧物流费用节约：
|
5 结束语
本文对较传统的船体车间设备布置进行了优化，在优化过程中是基于物流费用最低化来实现物料周转量较小化，从而较好地考虑了物料移动工作量与加工的便利性；这种思想与方法也适用于主流产品或工艺流程发生变化的设备布置优化。以后需要进一步扩展到三、四排列下的设备布置优化问题，这样更具普遍性。
参考文献:
［1］Kai-Yin Gau.Facility layout with an iterativealgorithm[D]. Auburn University. 32-38.
［2］邱枫,李波.基于单亲遗传算法的多行设备布置方法及仿真[J].哈尔滨商业大学学报(自科版),2007,23(1):124-128.
［3］张毕西,刘永清.多对象生产单元设备双行布置优化分析[J].华南理工大学学报(自科版),1999,27(5):45-51.
［4］张毕西,赵伟,廖朝辉.多对象生产系统设备多行布置优化.系统工程与电子技术,2004,26(6):754-756,858.
［5］都全.基于物流量最小的造船车间流程优化研究[J].江苏科技大学第四届研究生学术论坛论文集,2008,12:134-142.
2/2 首页 上一页 1 2 |
