标准化函数 被引入用来考虑应力状态对损伤发展的影响,被表示为: 被引入用来考虑应力状态对损伤发展的影响,被表示为:
 (5) (5)
其中 是平均应力,模型参数 是平均应力,模型参数 用来控制应力对损伤发展速度的影响, 用来控制应力对损伤发展速度的影响, 为材料抗压强度。参考Mazars的研究,采用如下的损伤准则: 为材料抗压强度。参考Mazars的研究,采用如下的损伤准则:
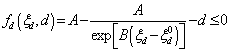 (6) (6)
参数 为材料破坏时可达到的最大损伤值; 为材料破坏时可达到的最大损伤值; 和 和 分别控制加载过程中损伤发展的速度和损伤发生阙值。 分别控制加载过程中损伤发展的速度和损伤发生阙值。
2.2剪切塑性的定义
根据试验结果发现水泥石的破坏面很大程度上取决于围压情况,线性破坏准则如莫尔库仑准则不能很好地反映实际情况。受Pietruszczak平方形式破坏准则的启发下,本文提出用多次方形式来描述屈服准则:
 (7) (7)
其中 是偏应力, 是偏应力, 为偏应力张量。 为偏应力张量。 和 和 是模型参数,用来决定破坏面的形状和位置; 是模型参数,用来决定破坏面的形状和位置; 反映材料受拉强度特性;参考压力 反映材料受拉强度特性;参考压力 ,取为1MPa,以保证A为无量纲参数。函数 ,取为1MPa,以保证A为无量纲参数。函数 反映材料硬化特征,由于损伤与塑性变形的同时存在和发展,函数 反映材料硬化特征,由于损伤与塑性变形的同时存在和发展,函数 的发展会出现不同的趋势:当损伤占主导作用时,材料显示脆性特征;当塑性变形为主要力学特征时,材料反映为塑性硬化。因此塑性硬化函数 的发展会出现不同的趋势:当损伤占主导作用时,材料显示脆性特征;当塑性变形为主要力学特征时,材料反映为塑性硬化。因此塑性硬化函数 表达为以下形式可以较好的体现这两种不同的趋势: 表达为以下形式可以较好的体现这两种不同的趋势:
 (8) (8)
其中 和 和 分别是初始塑性硬化值和塑性强化参数, 分别是初始塑性硬化值和塑性强化参数, 是因为剪切塑性引起的广义塑性变形,其增量形式表示为: 是因为剪切塑性引起的广义塑性变形,其增量形式表示为:
 (9) (9)
根据试验结果分析发现塑性硬化过程与围压大小相关联,因此引入函数 来控制环压对塑性强化速率的影响: 来控制环压对塑性强化速率的影响:
 (10) (10)
其中 为材料参数, 为材料参数, 为第三主应力,在本论文中体现为围压。当 为第三主应力,在本论文中体现为围压。当 时,屈服面 时,屈服面 与破坏面重合。 与破坏面重合。
水泥基材料如同绝大多数材料,关联的流动法则不能较好地反映塑性变形特征,参照Pietruszczak等的塑性模型,本文采用以下非关联塑性流动法则:
 (11) (11)
其中 通过 通过 求解获得,表示为 求解获得,表示为 坐标系中塑性势函数面与 坐标系中塑性势函数面与 轴交界处的值; 轴交界处的值; 定义了 定义了 坐标系中体积压缩-膨胀的转变面。根据试验结果, 坐标系中体积压缩-膨胀的转变面。根据试验结果, 可以用线性函数近似求解获得: 可以用线性函数近似求解获得:
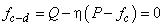 (12) (12)
2.3孔隙塑性的定义
Gurson于1977年提出了关于具有微小孔隙金属的塑性准则,近年来Leblond、Perrin等学者阐明了Gurson塑性准则的微观力学机理背景。因此,本文采用Gurson塑性屈服准则的一般形式来描述水泥石的孔隙塑性:
 (13) (13)
其中 是模型参数用来控制屈服面的形状; 是模型参数用来控制屈服面的形状; 表示材料的孔隙率,由于体积变形从而造成孔隙率变化,其增量形式可以表示为 表示材料的孔隙率,由于体积变形从而造成孔隙率变化,其增量形式可以表示为 ; ; 为塑性屈服应力硬化函数,其值随塑性发展情况而得到强化,根据静水压力试验结果, 为塑性屈服应力硬化函数,其值随塑性发展情况而得到强化,根据静水压力试验结果, 被表示为 被表示为
 (14) (14)
其中 是因为孔隙塑性机理产生的塑性体积应变, 是因为孔隙塑性机理产生的塑性体积应变, 是初始情况下的塑性屈服应力, 是初始情况下的塑性屈服应力, 、 、 和 和 是函数参数,用来控制硬化过程,可以通过静水压力试验数据获得。 是函数参数,用来控制硬化过程,可以通过静水压力试验数据获得。
相应的,孔隙塑性机理也采用流动法则来控制塑性发展过程,这里采用相关联的塑性流动法则:
 (15) (15)
2.4两种塑性共同作用过程
对于剪切塑性和孔隙塑性共同作用的情况,本构关系表示为:
 (16) (16)
本构关系可重写为增量形式:
 (17) (17)
塑性应变的增量形式可以被表示为:
 (18) (18)
其中 和 和 分别代表剪切塑性算子和孔隙塑性算子。考虑到力学损伤的作用,塑性相容条件可表示为: 分别代表剪切塑性算子和孔隙塑性算子。考虑到力学损伤的作用,塑性相容条件可表示为:
 (19) (19)
表达式(17)、(18)带入相容方程(19),整理可得相应情况下的剪切塑性算子 和孔隙塑性算子 和孔隙塑性算子 。 。
根据不同的加载过程,剪切塑性和孔隙塑性可能单独或同时产生,可以归结为以下4种情况:
(1) 并且 并且 ,两种塑性都没有产生。 ,两种塑性都没有产生。
(2) 、 、 并且 并且 ,产生剪切塑性变形,无孔隙塑性变形 ,产生剪切塑性变形,无孔隙塑性变形 。 。

(3) 并且 并且 、 、 ,无剪切塑性变形 ,无剪切塑性变形 ,产生孔隙塑性变形。 ,产生孔隙塑性变形。

(4) 、 、 并且 并且 、 、 ,剪切塑性变形和孔隙塑性变形同时产生。塑性算子 ,剪切塑性变形和孔隙塑性变形同时产生。塑性算子 和 和 可以在下列方程式解答中得到: 可以在下列方程式解答中得到:

其中 , , , , 。 。
图1是两种塑性共同作用示意图,可以看到在 平面中,剪切塑性破坏面与孔隙塑性屈服面表现为钝角状态相交,这样的相交形式可以保证在进行数值计算时收敛的稳定性。如图所示在低围压三轴试验的情况如单轴压缩试验时,加载路径只与剪切塑性面相联系,加载在达到孔隙塑性面之前已经破坏,孔隙塑性屈服面不参与塑性发展过程;随着围压的增加,中围压情况下,随着加载过程,剪切塑性机理先参与塑性发展,其后在加载达到一定程度时孔隙塑性机理共同控制塑性发展;而在高围压状态,孔隙塑性与剪切塑性机理共同参与到塑性发展中,其中孔隙塑性的影响决定了材料的主要变形特征。 平面中,剪切塑性破坏面与孔隙塑性屈服面表现为钝角状态相交,这样的相交形式可以保证在进行数值计算时收敛的稳定性。如图所示在低围压三轴试验的情况如单轴压缩试验时,加载路径只与剪切塑性面相联系,加载在达到孔隙塑性面之前已经破坏,孔隙塑性屈服面不参与塑性发展过程;随着围压的增加,中围压情况下,随着加载过程,剪切塑性机理先参与塑性发展,其后在加载达到一定程度时孔隙塑性机理共同控制塑性发展;而在高围压状态,孔隙塑性与剪切塑性机理共同参与到塑性发展中,其中孔隙塑性的影响决定了材料的主要变形特征。 2/5 首页 上一页 1 2 3 4 5 下一页 尾页 |


