论文摘要:本文首先进行了水泥石的三轴试验和静水试验,根据试验结果分析了宽围压范围下不同力学机理对水泥石宏观力学性能的影响。提出了基于热力学定律的剪切塑性、孔隙塑性与破坏准则相互作用的弹塑性损伤本构模型。该模型有效的考虑了围压对材料主要力学特征的影响,提出了与损伤准则相关联的塑性硬化函数。数值解答与试验结果比较表明,该本构模型可以很好地描述水泥石在低围压状态下的脆性、中围压下的脆-塑性转换以及高围压下的孔隙塑性为主的力学特征。
论文关键词:水泥基材料,宽围压范围,本构关系,塑性机理,损伤准则
引言
水泥基材料本构关系的研究对于土木和水利工程结构设计和安全性科学研究具有基础性的地位和意义。随着大型工程、地下工程以及国家安全工程的不断增多,结构所处的应力状态更加复杂,特别是三向受力情况。研究人员对复杂荷载情况下的材料本构关系愈加重视,如混凝土的多轴强度和本构关系是《混凝土结构设计规范》GB50010-2002中新增的主要内容之一。国内外学者在水泥基材料的试验和本构理论等方面开展了相关研究,Kupfer、Kotsovos等进行相关试验研究,表明混凝土的力学特征与围压状态相关,随着围压的增加,塑性应变成为混凝土材料最主要的力学特征。相关弹塑性本构模型也是科研人员关心的焦点,Dragon、Jefferson等人在论文中阐述了损伤准则与剪切塑性相互作用的塑性损伤本构模型,李杰、王怀亮、冷飞等学者就混凝土本构理论等方面开展了相关研究,提出的双标量损伤定义来有效解决混凝土的单边效应和多轴本构关系;同时,热力学定律下的损伤准则可以较好反映材料的非线性特征。法国里尔力学实验室进行了水泥石的试验研究,获得水泥石在静水压力以及宽围压下的三轴试验的应力-应变关系;在已有本构模型研究的基础上,结合其他准脆性材料的本构理论和损伤理论的研究,本文提出了剪切塑性机理与孔隙塑性机理共同影响,同时综合考虑损伤准则与塑性机理相互作用的宽围压范围的水泥基材料的本构模型。
1试验过程与试验数据分析
所有试验在法国里尔力学实验室完成,试验中采用长70mm直径36mm的圆柱体试件。水泥为G级(欧洲标准)普通硅酸盐水泥,水灰比为0.44。试样成型24h后脱模,放入20℃的水中养护27d后进行试验。试验设备为法国里尔科技大学研制的三轴仪。三轴仪配备了2路独立控制压力泵,压力泵最高可施加60MPa荷载。本试验中,1路压力泵用来控制轴压,1路压力泵控制围压。轴向位移用位移传感器测定,环向应变用应变环进行测定。静水压力试验采用应力加载模式对2路压力泵进行控制;对于三轴试验,现采用应力加载模式使试件处于初始受力状态,接着采用位移加载模式施加轴向荷载,直到试件失效破坏。本试验采用1MPa/min的应力加载速率和10/s的应变加载速率。
在如上描述的试验条件下,法国里尔力学实验室完成了相关试验,试验结果见图2至图5,图2至图4分别是水泥石在三个典型(低、中和高)围压下的应力-应变曲线,图5是水泥石在静水压力试验中的静水压力-体积应变曲线。从图中可以发现,围压对水泥石的力学特征有明显的作用。在低围压情况下,主要表现为脆弹性,在达到峰值后出现明显的软化段;在中围压情况下,弹塑性特征占主导地位,随着围压的增加,峰后软化现象消失;在高围压下,随着应变持续的施加,没有观测到应力峰值点的出现,在相当大的应变范围内,应力都持续增加,这有可能说明由于水泥石受到高压力作用使其内部孔隙收缩,在此过程中水泥石可承受荷载上升。静水压力试验结果证实了类似的观点,从图5中可以看出,在经历开始的弹性阶段后,随着应变的增加,在到达某一应力值,应力-应变曲线变化为非线性,体现为更高的体积压缩速率。这一试验现象和高围压三轴试验结果有类似之处,可以归结为非弹性的孔隙收缩现象。本文根据试验现象和试验数据的分析,拟建立考虑剪切塑性机理、孔隙塑性机理与损伤准则的水泥基材料的本构模型。
2模型描述和理论分析
根据以上试验结果分析,水泥石的力学特征可以用弹塑性损伤本构模型来描述。由于水泥石材料的均匀性,包括其他水泥基材料宏观上的各向同性和组分随机分布特征,本文认为材料表现为各向同性。因此热力学势能 可以表达为以下形式: 可以表达为以下形式:
 (1) (1)
 , , 代表弹性偏应变,其中四阶张量 代表弹性偏应变,其中四阶张量 和 和 分别定义为 分别定义为 , , , , 为二阶单位向量, 为二阶单位向量, 为对称四阶张量表达为 为对称四阶张量表达为 。 。 是弹性应变, 是弹性应变,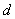 是损伤变量, 是损伤变量, 反映塑性硬化内变量, 反映塑性硬化内变量, 和 和 分别代表材料的有效体积模量和剪切模量, 分别代表材料的有效体积模量和剪切模量, 是塑性硬化能表示为塑性硬化内变量 是塑性硬化能表示为塑性硬化内变量 和力学损伤 和力学损伤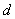 的函数。材料的有效弹性刚度四阶张量 的函数。材料的有效弹性刚度四阶张量 可以表示为 可以表示为 。 。
2.1力学损伤的定义
这里采用微观力学中稀疏解法的表达方式,考虑损伤情况的有效体积模量和剪切模量可以表示为:
 (2) (2)
 和 和 为无损伤情况下的材料初始体积模量和剪切模量,参数 为无损伤情况下的材料初始体积模量和剪切模量,参数 和 和 体现力学损伤对弹性特征的影响程度。由热力学势能对损伤变量的偏导数获得热力学伴随损伤量为: 体现力学损伤对弹性特征的影响程度。由热力学势能对损伤变量的偏导数获得热力学伴随损伤量为:
 (3) (3)
从式(3)中可以看到热力学伴随量只与弹性应变有关,对于压力作用下水泥石也具有塑性应变的特征,我们也将塑性应变考虑到其中;同时,认为在体积应变减小的情况下热力学伴随损伤量不会发生变化,对于损伤发展的等效损伤量 本文提出以下表达形式: 本文提出以下表达形式:
 (4) (4)
其中 是Macaulay符号,表示为当 是Macaulay符号,表示为当 时, 时, ;当 ;当 时, 时, 。 。
1/5 1 2 3 4 5 下一页 尾页 |


