 , , , (27) , (27)
其中 .此外,易证空穴表面的径向应力和环向应力分别为 .此外,易证空穴表面的径向应力和环向应力分别为
 , , (28) (28)
2.3 数值算例
为了进一步说明前面的结论,取 ,容易验证, ,容易验证, 满足条件(15).再根据线性化约束条件(10),得到 满足条件(15).再根据线性化约束条件(10),得到
 杂志网, 杂志网, , ,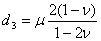 (29) (29)
为了保证 均为正,由 均为正,由
 (30) (30)
容易求得此种材料组成的柱体内部发生空穴分岔时的临界伸长为
 (31) (31)
图1示出了柱体内部空穴的生成和增长与给定的表面伸长和轴向伸长之间的关系(即空穴分岔曲线);图2示出了对于不同的表面伸长 的值,柱体内部的径向位移;图3示出了当表面伸长超过临界值时的应力间断;图4示出了对于不同的表面伸长 的值,柱体内部的径向位移;图3示出了当表面伸长超过临界值时的应力间断;图4示出了对于不同的表面伸长 的值,柱体内部的应力分布.注:在图1~4中, 的值,柱体内部的应力分布.注:在图1~4中, . .
 
图2 轴向伸长对圆柱体轴线上空穴生成 图3 对于不同的 的值,圆柱体内部的径 的值,圆柱体内部的径
和增长的影响向位移曲线
Fig.2 Effect of axial stretch on cavity formationFig.3 Curves of radialdisplacement for various
and growth ofcylindervalues of 
 
图4 空穴表面的应力间断 图5 柱体内部的应力分布
Fig.4 Discontinuity of stresses at the surface ofthe cavity Fig.5 Distribution of stresses in the interior ofthe
cylinder
3 结果分析
本文研究了由各向同性可压缩的广义Varga材料组成的实心圆柱体在给定的表面径向拉伸和轴向拉伸共同作用下的空穴分岔问题.给出了问题的参数型解析解;证明了当径向伸长超过某临界值时,柱体内部有空穴生成并快速增长(如图2所示),并且临界伸长随轴向伸长的增大而减小;由图3可见,当 时,即在空穴生成之前,整个柱体的变形是膨胀的;当 时,即在空穴生成之前,整个柱体的变形是膨胀的;当 时,即空穴生成后,空穴附近的变形是收缩的,而圆柱体表面附近是扩张的;由图4和图5可见,当 时,即空穴生成后,空穴附近的变形是收缩的,而圆柱体表面附近是扩张的;由图4和图5可见,当 时,径向应力和环向应力的分布都是均匀的;但是,当 时,径向应力和环向应力的分布都是均匀的;但是,当 时,柱体的均匀应力状态发生了突变,出现了应力间断现象,即从 时,柱体的均匀应力状态发生了突变,出现了应力间断现象,即从 的均匀分布应力状态转变为 的均匀分布应力状态转变为 时的非均匀分布应力状态.当 时的非均匀分布应力状态.当 时,环向应力随着变量 时,环向应力随着变量 的增大而迅速地减少,并且在空穴表面附近出现了明显的应力集中现象,对于环向伸长也有类似现象.正因为空穴表面附近的应力集中,才导致空穴的突然生成,这与实际的物理背景相吻合. 的增大而迅速地减少,并且在空穴表面附近出现了明显的应力集中现象,对于环向伸长也有类似现象.正因为空穴表面附近的应力集中,才导致空穴的突然生成,这与实际的物理背景相吻合.
参考文献
[1]Ogden R W. Nonlinear Elastic Deformations[M]. Ellis Horwood,Chichester, West Sussex, England, 1984.
[2]Gent A N, Lindley P B. Internal rupture of bonded rubbercylinders in tension[J]. Proc. R. Soc. London Ser A, 1958, 249 (1257): 195-205.
[3]Ball J M. Discontinuous equilibrium solutions and cavitations innonlinear elasticity [J]. Philos Trans Roy Soc Lond Ser A, 1982, 306 (3):557-610.
[4]Horgan C O, Polignone D A. Cavitation in nonlinear elasticsolids: A review [J]. Applied Mechanics Review, 1995, 48 (8):471-485.
[5]Yuan X G, Zhu Z Y, Cheng C J. Study on Cavitated Bifurcationproblems for Spheres Composed of Hyper-elastic Materials[J]. J. Engin. Math.,2005, 51(1): 15-34.
[6]Horgan C O. Void nucleation and growth for compressiblenon-linearly elastic materials: an example[J]. Int. J. Solids Structures, 1992,29 (3): 279-291.
[7]Murphy J G, Biwa S. Nonmontonic cavity growth in finite,compressible elasticity[J]. Int. J. Solids Structures, 1997, 34 (29): 3859-3872.
[8]Shang X C, Cheng C J. Exact Solution for cavitated bifurcationfor compressible hyper-elastic materials[J]. Int. J. Engin. Sci., 2001, 39 (10):1101-1117.
[9]Ren J S, Cheng C J. Cavitated bifurcation for composedcompressible hyper-elastic materials[J]. Acta Mechanica Solida Sinica, 2002,15 (2): 208-213.
[10]Carroll M M. Finite strain solutions incompressible isotropic elasticity[J] J. Elasticity, 1988, 20 (1): 65-92.
3/3 首页 上一页 1 2 3 |


