 和 和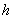 分别是主不变量 分别是主不变量 和 和 的非线性函数,且均为二次连续可微的;本文中,考虑如下一类特殊的可压缩超弹性材料模型,其应变能函数 的非线性函数,且均为二次连续可微的;本文中,考虑如下一类特殊的可压缩超弹性材料模型,其应变能函数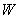 的形式为 的形式为
 (13) (13)
其中 是材料常数, 是材料常数,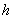 是二次连续可微的非线性函数.特别地,当 是二次连续可微的非线性函数.特别地,当 是 是 的线性函数时,式(13)称为可压缩的Varga材料模型[10],因此称式(13)为可压缩的广义Varga材料模型.由正规化条件(10),有 的线性函数时,式(13)称为可压缩的Varga材料模型[10],因此称式(13)为可压缩的广义Varga材料模型.由正规化条件(10),有
 , , (14) (14)
其中 表示对宗量 表示对宗量 的导数.另一方面,为了确保材料的力学行为的合理性,应变能函数还必须满足强凸性条件[1],从而有 的导数.另一方面,为了确保材料的力学行为的合理性,应变能函数还必须满足强凸性条件[1],从而有
 (15) (15)
至此,由各向同性可压缩的广义Varga材料模型(13)组成的圆柱体在给定的表面径向伸长  和轴向拉伸(压缩) 和轴向拉伸(压缩) 共同作用下的轴对称变形问题的数学模型由基本控制方程(5)、应变能函数(13),边界条件(7)和(8)组成. 共同作用下的轴对称变形问题的数学模型由基本控制方程(5)、应变能函数(13),边界条件(7)和(8)组成.
2 控制方程的解及其定性分析
2.1 参数型解析解和空穴分岔解
显然杂志网,对任意给定的 ,控制方程的一个平凡解(称为均匀变形解)为 ,控制方程的一个平凡解(称为均匀变形解)为
 (16) (16)
它对应于柱体内部的径向位移 . .
将式(13)代入到方程(5),则有
 (17) (17)
其中 由式(12)3给出.由式(2)可知 由式(12)3给出.由式(2)可知 ,且根据式(15),从而得到 ,且根据式(15),从而得到
 (18) (18)
其中 是一个积分常数.由式(18)不难得到径向变形函数的通解形式为 是一个积分常数.由式(18)不难得到径向变形函数的通解形式为
 (19) (19)
其中 也是一个积分常数. 也是一个积分常数.
下面利用边界条件(7)和(8)确定积分常数 和 和 .由外边界条件(7)得 .由外边界条件(7)得
 (20) (20)
进一步地,将式(13)代入到式(6)1,得到
 (21) (21)
由式(19)可得 .由式(21)和内边界条件(8)得 .由式(21)和内边界条件(8)得
 (22) (22)
综合上面的分析可知,对于任意给定的 ,由式(19)和(22)知, ,由式(19)和(22)知, ,即 ,即 是方程(22)的一个解,它对应于柱体内部均匀变形解 是方程(22)的一个解,它对应于柱体内部均匀变形解 ;若存在 ;若存在 ,使得 ,使得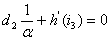 ,则 ,则 可由 可由 求得,即满足边界条件的控制方程(5)有两个解,除平凡解外,还有一个非平凡解(19). 求得,即满足边界条件的控制方程(5)有两个解,除平凡解外,还有一个非平凡解(19).
至此,对应于由可压缩的广义Varga材料(13)组成的实心圆柱体,式(19)便为在给定的径向拉伸 和轴向伸长共同作用下的轴对称变形问题的精确解. 和轴向伸长共同作用下的轴对称变形问题的精确解.
在圆柱体轴线上,对于任意给定的 , , 是方程(22)的一个解,称之为方程(22)的平凡解;另一方面,可以求得圆柱体内部有空穴生成时的临界伸长为 是方程(22)的一个解,称之为方程(22)的平凡解;另一方面,可以求得圆柱体内部有空穴生成时的临界伸长为
 (23) (23)
即方程(22)在临界点  处从平凡解 处从平凡解 处发生分岔,非平凡解 处发生分岔,非平凡解 (代表空穴生成后的半径),其中 (代表空穴生成后的半径),其中 ,且 ,且 由方程 由方程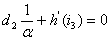 确定,从而称(22)为空穴分岔方程. 确定,从而称(22)为空穴分岔方程.
另一方面,当 时,与均匀变形解相对应的径向位移为 时,与均匀变形解相对应的径向位移为
 (24) (24)
当 时,与空穴生成后的解 时,与空穴生成后的解 相对应的径向位移为 相对应的径向位移为
 (25) (25)
2.2 柱体内部的应力分布
下面讨论柱体内部发生空穴分岔时的应力分布.
当 时,对应于均匀变形解 时,对应于均匀变形解 ,有 ,有 , , ,因此柱体内部的径向应力环向应力相等,即 ,因此柱体内部的径向应力环向应力相等,即
 (26) (26)
当 时, 时, ,径向应力和环向应力分别为 ,径向应力和环向应力分别为
2/3 首页 上一页 1 2 3 下一页 尾页 |


