论文导读::对于由一类均匀各向同性可压缩的广义Varga材料组成的实心圆柱体,研究其在给定的外表面拉伸和轴向拉伸或压缩共同作用下的轴对称变形问题.利用能量变分原理得到了问题的控制方程和边界条件,并求得了描述柱体径向对称变形的参数型解析解和描述圆柱体轴线上空穴生成和增长的空穴分岔解.给出了与泊松比和轴向伸长相关的径向临界伸长的表达式和空穴生成后的应力表达式;并通过数值算例讨论了这些参数对圆柱体轴线上空穴生成和增长、圆柱体的径向位移以及应力的集中和突变的影响,同时给出了相应的数值模拟.
论文关键词:可压缩超弹性材料,轴对称变形,轴向伸长,应力的集中和突变,空穴分岔
0 引言
橡胶和类橡胶材料在现实生活中的应用是有目共睹的.由于这些材料的制品都是在一定环境和载荷下使用的,因此它们都会遇到变形、失稳、使用寿命有限以及破坏等问题.从力学性能上讲,橡胶和类橡胶材料具有复杂的分子特性以及材料和几何的双重非线性性质,这些材料同时又称为超弹性材料或Green弹性材料,它们的本构关系可完全由其应变能函数表示[1].在涉及超弹性领域的众多问题中,材料和结构的不稳定性一直是人们关注的焦点,而材料中空穴的生成、增长以及相邻空穴的贯通是材料局部损伤和破坏的重要机理.在实验方面,文献[2]早在1958年便证实了硫化橡胶材料内部有空穴突然生成的现象.但是在理论研究方面,直到1982年才由文献[3]将空穴的生成与增长归结为一个数学模型的分岔问题.文献[4]和[5]对近些年来关于橡胶和类橡胶材料中空穴现象在理论方面的研究进展进行了综述.特别地,文献[6~9]研究了几类可压缩超弹性球体中的空穴现象,并且给出了轴对称变形问题的解析解以及空穴分岔解.然而,对于不同类型的可压缩超弹性材料,由于其对应的应变能函数形式有所不同,从而导致研究方法有很大的差异,所研究的问题是否存在解析解也是不可预知的.本文的目的是研究可压缩的超弹性圆柱体在径向拉伸和轴向拉伸或压缩的共同作用下,圆柱体轴线上的空穴现象,其中圆柱体是由一类可压缩的广义Varga材料组成的.首先建立了轴对称变形问题的数学模型;然后求得了问题的参数型解析解和空穴分岔解,以及径向应力和环向应力的表达式;最后通过数值算例讨论了轴向伸长对圆柱体轴线上空穴的伸长和增长的影响,并且对圆柱体内部的径向位移、应力的集中和突变进行了相应的数值模拟.
1 问题的数学描述
1.1 控制方程和边界条件
假设半径为 的无限长实心圆柱体由均匀各向同性的可压缩超弹性材料组成,考察圆柱体在外表面均布的径向拉伸和轴向拉伸或压缩共同作用下的有限变形问题(如图1所示).在柱坐标系下,变形前后的柱体中的点分别表示为 的无限长实心圆柱体由均匀各向同性的可压缩超弹性材料组成,考察圆柱体在外表面均布的径向拉伸和轴向拉伸或压缩共同作用下的有限变形问题(如图1所示).在柱坐标系下,变形前后的柱体中的点分别表示为 和 和 ,并且取坐标系的原点在圆柱体横截面的中心处.在径向对称变形的假设下杂志网,变形分量和主伸长分别表示为 ,并且取坐标系的原点在圆柱体横截面的中心处.在径向对称变形的假设下杂志网,变形分量和主伸长分别表示为
![一类可压缩超弹性圆柱体轴线上的空穴现象[*] 轴向伸长](/d/file/picture/201304/03/18.files/image004.gif) (1) (1)
![一类可压缩超弹性圆柱体轴线上的空穴现象[*] 轴向伸长](/d/file/picture/201304/03/18.files/image005.gif) (2) (2)
其中 是待求的径向变形函数, 是待求的径向变形函数, 是预先给定的轴向伸长, 是预先给定的轴向伸长, 表示关于自变量 表示关于自变量 的导数.容易看到,若 的导数.容易看到,若 ,则圆柱体在现时构形中仍是实心的;若 ,则圆柱体在现时构形中仍是实心的;若 ,则在圆柱体的轴线上有半径为 ,则在圆柱体的轴线上有半径为 的圆柱形空穴生成,此时假设空穴表面是无约束的. 的圆柱形空穴生成,此时假设空穴表面是无约束的.
![一类可压缩超弹性圆柱体轴线上的空穴现象[*] 轴向伸长](/d/file/picture/201304/03/18.files/image013.gif) 此外,为了确保变形是径向对称的,在 此外,为了确保变形是径向对称的,在 上必须有 上必须有 ,于是由式(2)得到 ,于是由式(2)得到
 (3) (3)
圆柱体变形后的总势能为
 (4) (4)
其中 是组成圆柱体的 图1 实心圆柱体受径向拉伸和轴向伸长作用的示意图 是组成圆柱体的 图1 实心圆柱体受径向拉伸和轴向伸长作用的示意图
可压缩超弹性材料的应变能函数.由式(2) Fig.1 Sketch map of solid cylinder under radialtension and
可知,总势能(4)是关于 的函数. axial stretch 的函数. axial stretch
由能量变分原理并结合式(2),可得如下的Euler-Lagrange方程
 (5) (5)
对应于径向对称变形的Cauchy应力张量的主元素为
 , , (6) (6)
假定在圆柱体的外表面上给定径向伸长  ,于是有边界条件 ,于是有边界条件
 (7) (7)
在圆柱体中心满足的边界条件为
 (8) (8)
式(8)表示:若圆柱体内部没有空穴生成,则 ;若在圆柱体中心有空穴生成,即 ;若在圆柱体中心有空穴生成,即 ,则对不受约束的空穴表面,有 ,则对不受约束的空穴表面,有 . .
1.2 应变能函数
众所周知,各向同性超弹性材料的本构关系可以完全由其应变能函数
 (9) (9)
来描述,其中 是应变张量的主值, 是应变张量的主值, 是 是 的对称函数.在自然状态下,为了保证各向同性的超弹性材料对应的应变能函数的线性化与经典的线性理论一致,应变能函数 的对称函数.在自然状态下,为了保证各向同性的超弹性材料对应的应变能函数的线性化与经典的线性理论一致,应变能函数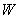 应满足的如下的约束条件[1] 应满足的如下的约束条件[1]
  , , , , (10) (10)
这里 和 和 分别为材料的剪切模量和泊松比, 分别为材料的剪切模量和泊松比, , , , , .此外,将应变能函数表示为应变张量的主不变量 .此外,将应变能函数表示为应变张量的主不变量 和 和 的函数[10],即, 的函数[10],即,
 (11) (11)
其中
 , , , ,  (12) (12)
1/3 1 2 3 下一页 尾页 |


