
成立。因此,结论得证。
推论2.2 给定概率空间 及其上的布朗运动 及其上的布朗运动 。对 。对 ,假定随机过程 ,假定随机过程 满足随机微分方程 满足随机微分方程
 , ,
其中 ,在给定条件下,有下面的结果成立 ,在给定条件下,有下面的结果成立
 。 。
证明:令 ,则由 ,则由 公式, 公式, 满足随机微分方程 满足随机微分方程
 , ,
则由文献[3],可得
 。 。
这就证得推论。
定理1.1 的证明:首先,不妨设 ,否则 ,否则 满足常微分方程 满足常微分方程
 。 。
可得 ,显然, ,显然,
 。 。
下面只需在 时进行证明。 时进行证明。
因为 满足随机微分方程 满足随机微分方程 ,则 ,则
 其中 其中 。 。
显然 是布朗运动。 是布朗运动。
令 ,则由 ,则由 公式知 公式知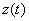 满足随机微分方程 满足随机微分方程
 , ,
所以由推论2.2可得
 。 。
显然
 。 。
下面在 上对随机微分方程 上对随机微分方程 进行积分, 可得 进行积分, 可得

在上式两端同除 整理后可得 整理后可得
下面只需证明 等式右边四项都几乎处处收敛到 等式右边四项都几乎处处收敛到 即可。为了证明 即可。为了证明 和 和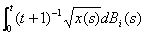  几乎处处收敛到 几乎处处收敛到 ,由引理2.1知只需证明 ,由引理2.1知只需证明 和 和  几乎处处存在即可。 几乎处处存在即可。
下面定义一列停时:

因为 ,所以存在 ,所以存在 ,使得 ,使得 ,同时也可知 ,同时也可知 a.e.。 a.e.。
事实上,

因此 ,所以下面只需证明 ,所以下面只需证明  在 在 上几乎处处存在,又因为 上几乎处处存在,又因为  是随机变量,故只需验证 是随机变量,故只需验证  都是 都是 有界鞅即可。 有界鞅即可。
事实上,

显然 是 是 有界鞅。 有界鞅。
为了证明 的第四项几乎处处收敛到 的第四项几乎处处收敛到 ,由 ,由 公式, 可得 公式, 可得 满足随机微分方程 满足随机微分方程

其中
显然我们可得
在 两端同除 两端同除 得 得
显然 。 。
为了证明 和 和  几乎处处收敛到 几乎处处收敛到 , 再次运用引理2.1知只需证明 , 再次运用引理2.1知只需证明 和 和  几乎处处存在,即证明 几乎处处存在,即证明 和 和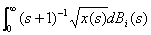  几乎处处存在,而由前面的证明知这是显然的。 几乎处处存在,而由前面的证明知这是显然的。
下面只需要证明 式中的第二项,即 式中的第二项,即
 。 。
又因为 ,所以对 ,所以对 ,有 ,有
 , ,
并且由

和 ,可知 ,可知
 。 。
而且

所以
 。 。
综上,结论得证。
参考文献:
[1]Deelstra, G., Long-term returns instochastic interest rate models: applications. [C]. Proc. 5th AFIR Int.Colloquium, Brussels, Belgium, 1995, 709-730.
[2]Deelstra, G., Long-term returns in stochasticinterest rate models: applications. [J] Astin Bulletin, 2000, Vol 30, No 1,123-140.
[3]Deelstra, G. and Delbaen, F., Long-termreturns in stochastic interest rate models. [J]. Insurance: Mathematics andEconomics, 1995, 17, 163-169.
[4]Deelstra, G. and Delbaen, F., Long-termreturns in stochastic interest rate models: different convergence results. [J].Applied Stochastic Models and Data Analysis, 1998, 13 No 3-4, 401--407.
[5]Duffie, D., Filipovic, D. andSchachermayer, W., Affine processes and applications in finance. [J]. Annals ofApplied Probability, 2003, 13, 984-1053.
[6]Dawson, D.A. and Li, Z.H., Skewconvolution semigroups and affine Markov processes. [J]. The Annals ofProbability, 2006, 34 (3), 1103-1142.
2/2 首页 上一页 1 2 |


