论文导读::本文建立新的风险模型,同时考虑干扰项和副索赔,对此模型给出了破产概率所满足的一般表达式和破产概率上界.
论文关键词:破产时刻,破产概率,条件概率,破产概率上界.
0 引言
经典风险模型未考虑到随机因素对盈余的影响,且不存在相依副索赔;文献[1]给出了经典模型破产概率所满足的表达式以及Lundberg上界,文献[2]和[3]在经典模型中加入了干扰项,分别得到了有干扰项时破产概率的表达式和Lundberg上界,文献[4]在经典模型基础上考虑了带有副索赔的情形,本文在此基础上,同时考虑干扰项和副索赔,重新建立了一个完全离散的风险模型,其中干扰项为一离散的布朗运动,以往文献中的干扰项一般都是连续的布朗运动.对此模型给出了破产概率所满足的一般表达式和破产概率上界.
1模型建立
考虑一个主索赔 ,一个与主索赔相关的副索赔 ,一个与主索赔相关的副索赔 和一个干扰项 和一个干扰项 ,当主索赔 ,当主索赔 发生,且 发生,且 (阀值)时,即发生副索赔 (阀值)时,即发生副索赔 .定义如下风险模型: .定义如下风险模型:

其中: 破产时刻, 破产时刻, 为保险公司初始准备金, 为保险公司初始准备金, 为保费率, 为保费率, 为离散的布朗运动,满足(1) 为离散的布朗运动,满足(1) ,(2) ,(2)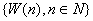 有平稳独立增量,(3)对每一个 有平稳独立增量,(3)对每一个 , , 服从正态分布,均值为 服从正态分布,均值为 ,方差为 ,方差为 , , 为正常数. 为正常数.
 , , , , 相互独立,且主索赔序列 相互独立,且主索赔序列 独立同分布,副索赔序列 独立同分布,副索赔序列 独立同分布, 独立同分布, , , , , , , .对于任意分布函数 .对于任意分布函数 ,记 ,记 . .
记破产时刻 ,破产概率为 ,破产概率为 . .
为保证保险公司的稳定经营,假定

定义调节系数 为下列方程的正数解: 为下列方程的正数解: . .
引理 2.1 方程 存在一正解 存在一正解 . .
证明:考虑如下两式
 (1) (1)
 (2) (2)
当 时,(1)式为 时,(1)式为 ,于是函数 ,于是函数 在 在 处某邻域内单调递减;并且(2)式表明函数 处某邻域内单调递减;并且(2)式表明函数 的图形是凸的,于是在 的图形是凸的,于是在 上必存在一 上必存在一 ,使得 ,使得 .示意图如下: .示意图如下:

定理 2.1 对于上述模型有:
证明: 利用条件期望有:
 (3) (3)
因 ,(3)式左端为: ,(3)式左端为:

同时 也可写为 也可写为 (4) (4)
取 使得 使得 ,将(4)式代入(3)式,有 ,将(4)式代入(3)式,有


同理

则(3)式可化为
 (5) (5)
当 时,(5)式右端第一项 时,(5)式右端第一项

下面证明破产时刻,当 时,(5)式右端第二项收敛于零 时,(5)式右端第二项收敛于零
首先给出,

1/2 1 2 下一页 尾页 |


