把3）变换为：
由于投资在项目寿命期内可能发生多次，并且投资属于项目外生，因此，可先将各期投资按基准折现率折算为现值，然后再考虑投资现值投入项目后的收益情况，上式可改写为：
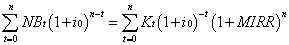 4）
4）式求解的MIRR唯一，MIRR即为修正内部收益率，且此方程诸如a(1+x)=b，求解非常简单。用MIRR指标来评价投资方案经济效益时，与外部收益率一样，需要与基准折现率i比较。其判别准则为：当MIRR≥i，项目可以被接受；反之，则拒绝。
2.2三种修正方法的比较
三种方法的共同点是：（1）都是从调整现金流量入手，且都把部分正净现金流量按基准折现率i等值到项目期末；（2）判断项目是否可行的标准一样，即都要与基准折现率i相比较；（3）都解决了传统内部收益率无解或者多解选择的问题；（4）三种方法只调整项目的现金流量，并未改变项目的本质，所以它与传统的内部收益率法具有同样的效果，与传统内部收益率法具有一致性（后文将从数学上证明这一点）。
三种方法的不同点是：（1）调整现金流量的范围不一样，现金流量转换法是将项目现金流量中最后一次出现负净现金流量前的所有正净现金流量按照既定的基准折现率等值转换到项目的末期；外部收益率法是把项目的净收益、即正净现金流量按照既定的基准折现率等值转换到项目的末期，调整范围更广；修正内部收益率法不仅把正净现金流量按照既定的基准折现率等值转换到项目的末期，而且还把投资，既把负净现金流量按照既定的基准折现率等值转换到项目的初期后再考虑投资的收益率，调整范围最广；（2）计算简易程度不一样，现金流量转换法的计算过程还是沿用传统的内部收益率计算中常用的直线插入法，一方面计算复杂，另一方面有一定的误差；虽然外部收益率方程的解是唯一的，可以解决IRR方程无解或多个情况，但当投资次数多时计算过程依然比较复杂。而修正外部收益率计算过程最简单，既避免了内部收益率无解或者多解的问题，又减少了误差。
2.3案例分析
某项目净现金流量如下表1所示，基准折现率i=10%。
表1（单位：万元）
|
年份（年末）
|
0
|
1
|
2
|
3
|
4
|
5
|
|
净现金流量
|
1900
|
1000
|
-5000
|
-5000
|
2000
|
6000
|
该项目是一个非常规现金流量项目，净现金流量符号改变两次，其IRR方程有两个解：i=10.2%，i=47.3%，用递推公式可判断10.2%是该项目的内部收益率，但计算量大。下面分别用上述三种方法求解：
⑴现金流量转换法
为使净现金流量符号只改变一次，把最开始两年初出现的正净现金流量用基准折现率折现到第5年末。第5年末净现金流量NCF=1900（1+10%）+1000（1+10%）+6000=10524.07万元。现金流量转换位下表4。
表4（单位：万元）
|
年份（年末）
|
0
|
1
|
2
|
3
|
4
|
5
|
|
净现金流量
|
0
|
0
|
-5000
|
-5000
|
2000
|
10524.07
|
折现到第2年末有：NPV=14.33万元，NPV=-379.07万元，直线插入法算得内部收益率 =10.07>i，项目可行。
⑵外部收益率法
据3）式列出如下方程：
1900（1+10%）+1000（1+10%）+2000（1+10%）+6000=5000(1+ERR)+5000(1+ERR)
解得：ERR=10.10%，ERR>i，项目可行。
⑶修正内部收益率法。
据4）式列出如下方程：
1900（1+10%）+1000（1+10%）+2000（1+10%）+6000=5000(1+10%)(1+MIRR)+5000(1+10%)(1+MIRR)
解得：MIRR=10.03%，MIRR>i，项目可行。
3非常规现金流量项目内部收益率法修正的一致性分析
从上例中可看出项目可行，且有IRR>IRR’>i；IRR>ERR>i；IRR>MIRR>i。但是，IRR≠IRR’≠ERR≠MIRR。因此，有必要探讨在判断项目是否可行时IRR与IRR’、IRR与ERR、IRR与MIRR的一致性。当IRR=i时，由2）、3）、4）式很容易得知：IRR=IRR’=ERR=MIRR=i；下面讨论IRR≠i时的情形。
3.1IRR与的一致性
借助集合来表示现金流方向不同的年份， , 表示项目在寿命周期内净现金流量为正的年份的集合； 表示项目在寿命周期内净现金流量为负的年份的集合。 为每个或每段负净现金流量出现前正净现金流量所对应的年份的集合， 为最后一个或一段负净现金流量出现后紧接的正净现金流量所对应的年份的集合， ；且 ， 。 表示第t年的正净现金流量， 表示第t年的负净现金流量，表示现金流量转换法求解的内部收益率。则现金流量转换法的求解公式用终值形式可表示为： 5）
当IRR>i时，根据IRR与NPV评价法的一致性，有NPV(i)>0，即： ，变换得：
 6）
6）-5）得：
由于终值函数是单调递增函数，所以得出 。 2/3 首页 上一页 1 2 3 下一页 尾页 |
