论文导读::本文重点介绍多种无线信道建模方法及其缺陷,给出一种基于MEDS-SP瑞利衰落信道模型的莱斯衰落信道改进模型,与此同时针对地空信道特性,从而建立适用于多种环境下的地空信道模型,这对研究地空信道传输性能具有重要意义。
关键词:瑞利衰落,莱斯衰落,MEDS-SP
地空通信是指空中飞行平台(如有人飞机等)与地面站之间的通信,其用于保障空中飞行平台与地面站之间交换信息和共享情报,使得地面站对空中飞行平台实时监视和指挥引导,提高空中飞行平台的生存能力。由于地空信道易受多径衰落和多普勒频移的影响,因此研究地空信道特性是提高地空通信系统性能的一个关键因素,同时能够有针对性地克服信道固有缺陷,从而发挥信道特有的优势。
1 地空信道特性
信号在地空通信系统中传播易受环境例如房屋、高山、雨雪和云层的影响而产生反射、衍射和绕射等现象。由此,接收信号的幅度将急剧变化,即产生了衰落。这种衰落是由多径引起的,也称为多径衰落。多径衰落分为平坦衰落和频率选择性衰落,,当衰落继续增大时,则会出现了严重的码间干扰(ISI)。
地空通信系统中通信链路始终保持“通视”效果,即直射分量依然存在,但由于信道的多径效应和多普勒效应等特性,使得接收信号还包括多径分量,信号的包络 服从莱斯分布,莱斯分布的概率密度函数如下: 服从莱斯分布,莱斯分布的概率密度函数如下:
 (1) (1)
式(1)中, 是直射分量的功率, 是直射分量的功率, 是多径分量的平均功率, 是多径分量的平均功率, 是第一类零阶修正贝塞尔函数。定义莱斯因子K为直射分量功率与多径分量平均功率的比值,即 是第一类零阶修正贝塞尔函数。定义莱斯因子K为直射分量功率与多径分量平均功率的比值,即 ,随着通信距离的增大和飞行器飞行速度的增加,直射分量功率逐渐降低,莱斯因子K也随之减小。通常在地空通信中瑞利衰落,莱斯因子在(2-20dB)范围内变化[1],当莱斯因子K小于等于6dB时,地空信道呈现低莱斯因子衰落特性。 ,随着通信距离的增大和飞行器飞行速度的增加,直射分量功率逐渐降低,莱斯因子K也随之减小。通常在地空通信中瑞利衰落,莱斯因子在(2-20dB)范围内变化[1],当莱斯因子K小于等于6dB时,地空信道呈现低莱斯因子衰落特性。
当 时,则表示没有直射分量,接收信号包络 时,则表示没有直射分量,接收信号包络 由莱斯分布转变为瑞利分布,如式(2)所示为瑞利分布的概率密度函数 由莱斯分布转变为瑞利分布,如式(2)所示为瑞利分布的概率密度函数
 (2) (2)
由此可知,瑞利分布是莱斯分布的一个特例;莱斯分布是瑞利分布的一个扩展。
2 莱斯平坦衰落信道的建模
多径衰落会引起接收信号在时域上的扩展,当发送信号的带宽足够窄,那么发送信号的所有频率分量几乎经历相同的衰落,此时信号在传输过程中将不会产生失真,这样的衰落称为是平坦衰落期刊网。
针对广义平稳特性和各态历经特性不能同时满足的问题,M.P?tzold在参考文献[2]中提出MEDS-SP确定型仿真模型,该仿真模型是对MEDS仿真模型中的离散多普勒频率进行改进,引入仿真次数因子,即多普勒系数和离散多普勒频率在仿真过程中是确定值,因此该模型不仅满足广义平稳特性还满足各态历经特性,且大大降低了仿真运算的复杂度,提高了仿真效率,是一种新的高效信道仿真模型。
MEDS-SP仿真模型的数学模型[2]如下:
 (3) (3) , , (4) (4)
其中, , , , , 分别表示幅度,信号到达角和初始相位; 分别表示幅度,信号到达角和初始相位; 为最大多普勒频率,由前面分析可知合理设置( 为最大多普勒频率,由前面分析可知合理设置( , , , , )这三个参数,就可以使仿真模型的统计特性与Clarke参考模型的相匹配,并满足广义平稳特性和各态历经特性。由于现有的信道仿真模型都不能很好的与Clarke参考模型的相匹配,故MEDS-SP仿真模型在MEDS仿真模型的基础上,对以上的三个参数进行了修改,如下所示: )这三个参数,就可以使仿真模型的统计特性与Clarke参考模型的相匹配,并满足广义平稳特性和各态历经特性。由于现有的信道仿真模型都不能很好的与Clarke参考模型的相匹配,故MEDS-SP仿真模型在MEDS仿真模型的基础上,对以上的三个参数进行了修改,如下所示:
 , , , ,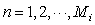 (5) (5)
 对所有的n都是在(-π, π]范围内均匀分布的随机变量, 对所有的n都是在(-π, π]范围内均匀分布的随机变量,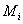 为正弦波数目,并且有 为正弦波数目,并且有 ;L为仿真次数, ;L为仿真次数, 。由式(4)可以看出,对于给定的 。由式(4)可以看出,对于给定的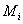 和L, 和L, 和 和 在仿真中是确定值,因此该模型产生的信号是满足各态历经特性的。 在仿真中是确定值,因此该模型产生的信号是满足各态历经特性的。
现基于MEDS-SP确定型仿真模型对莱斯衰落信道模型进行改进如下:
 (6) (6)
 (7) (7) (8) (8)
上式中K为莱斯因子, 和 和 分别是直射分量的到达角和初始相位,其中 分别是直射分量的到达角和初始相位,其中 在(-π, π]内均匀分布,并且复高斯随机过程 在(-π, π]内均匀分布,并且复高斯随机过程 的包络 的包络 服从莱斯分布,相位服从(-π, π]范围内的均匀分布。 服从莱斯分布,相位服从(-π, π]范围内的均匀分布。
3统计特性仿真与分析
由于在正弦波数目和仿真次数趋于无穷时,现有的仿真模型产生的信号的包络均服从瑞利分布,相位均服从(-π, π]的均匀分布,因此下面首先通过实验仿真对比Yahong R.Zheng和Chenshan Xiao分别在参考文献[3]、[4]和[5]中提出的三种随机型仿真模型(记为模型Ⅰ、模型Ⅱ和模型Ⅲ)以及MEDS-SP确定型仿真模型(模型Ⅳ)的相关统计特性,如图2.1-图2.4所示。仿真条件为:载频fc=2000MHz,移动速度v=150Km/h,抽样时间fmaxτ=0.01s,M代表仿真的正弦波数瑞利衰落,L代表仿真次数。
对比图2.1和图2.2可知,模型Ⅳ的相关统计特性在正弦波数目M和仿真次数L较小的情况下就能与Clarke参考模型相匹配,而其他三种模型的自相关即使在仿真次数L很大的情况下(如L=100时)也不能与参考模型完全吻合,这是由于模型Ⅳ在离散多普勒频率中引入仿真次数因子L的缘故;图2.3中,模型Ⅳ由于两路正弦波数目 ,所以其互相关为0,而其他三种模型的互相关均不为0。图2.4表明这四种仿真模型均满足广义平稳特性,并且模型Ⅰ、Ⅱ和Ⅳ与参考模型最匹配,而模型Ⅲ的复信号自相关函数值是理想参考模型的一半。 ,所以其互相关为0,而其他三种模型的互相关均不为0。图2.4表明这四种仿真模型均满足广义平稳特性,并且模型Ⅰ、Ⅱ和Ⅳ与参考模型最匹配,而模型Ⅲ的复信号自相关函数值是理想参考模型的一半。
综上所述,模型Ⅳ即MEDS-SP确定型仿真模型要优于现有的其他衰落信道仿真模型,现对莱斯衰落信道改进模型的统计特性进行仿真,如下图2.5-图2.7所示。从仿真图可以看出,改进型莱斯衰落信道仿真模型的一阶和二阶统计特性均与理想莱斯衰落过程吻合,不仅满足实际信道要求,还具有高精度和低仿真运算复杂度的优点。
 
图2.1 M=10,L=4时同相自相关线 图2.2 M=10,L=100时同相自相关曲线
 
图2.3 M=50,L=10时互相关曲线 图2.4M=10,L=10时复信号自相关曲线
 
图2.5不同K的复信号自相关的实部 图2.6不同K值时复信号包络的概率密度

图2.7 M=8,θ0=π/4,L=10时不同K的电平通过率
4 结束语
本文对地空信道的建模进行了一个比较全面的分析,首先从概念上介绍地空通信信道的主要特性和信道的衰落;其次重点研究莱斯平坦衰落信道的建模,给出MEDS-SP瑞利高效信道模型的同时,并在该模型的基础上对莱斯衰落信道模型进行改进,实验仿真表明新改进型莱斯衰落信道模型与理想莱斯衰落过程吻合,不仅满足实际信道要求,还具有高精度和低仿真运算复杂度的优点。
参考文献
[1]A. Neul et al.. PropagationMeasurements for the Aeronautical Satellite Channel[C]. IEEE VTC .1987:90-97.
[2]M.P?tzold, B. Hogstad and D Kim .A New Design Concept for High-Performance FadingChannel Simulators Using Set Partitioning[J].Wireless Personal Communications,2007,40(3):267-279.
[3]Y. R.Zheng and C. Xiao. Improved Models for the Generation of Multiple UncorrelatedRayleigh Fading Waveforms[J]. IEEE Commun.2002, 6(6):256-258.
[4]Y. R.Zheng and C. Xiao. Simulation Models with Correct Statistical Properties forRayleigh Fading Channels [J]. IEEE Trans Communications, 2003, 51(6): 920-928.
[5]C.Xiao, Y. R. Zheng and N. C. Beaulieu. Novel Sum-of-Sinusoids Simulation Models forRayleigh and Rician Fading Channels[J]. IEEE Trans Wireless Commun, 2006,5(12):3667-3679.
|


