摘要:采用线性组合算符、变分相结合的方法和采用改进的线性组合算符、变分相结合的方法研究了无限深量子阱中弱耦合束缚极化子的性质。导出了无限深量子阱中束缚极化子的基态能量随库仑束缚势、阱宽和拉格朗日乘子的关系。通过数值计算结果表明:基态能量随着库仑束缚势、阱宽和拉格朗日乘子的增大而减小。
论文关键词:量子阱,线性组合算符,束缚极化子,基态能量
近年来,随着材料生长的技术发展,尤其是纳米技术飞速发展,极大地推进了对低维系统的广泛研究。人们利用分子束外延技术(MBE)、金属有机化学气相技术(MOCVD) 和化学自组装技术等已经可以制造出各种如量子点、量子阱和量子线等纳米结构。这是半导体物理及材料科学的重大突破。量子阱中的电子在一个方向上受到很强的限制,因此,和晶体相比较,量子阱中的束缚极化子效应更加明显。所以量子阱中的束缚极化子引起了学者们的广泛研究[1~3],Chen 等[4]运用 Landau - Pekar 变分法研究了量子阱中束缚极化子的基态性质。Comas等[5]和Buacker等[6]运用标准的微扰理论讨论了量子阱中极化子和磁极化子的自能。Ren 等[7]运用 Feynman-Haken 路径积分理论计算了处于库仑势中抛物量子阱内极化子的基态能量。Stopa 等[8]运用数值求解薛定谔方程的方法 ,计算了基态能量和激发态结合能。刘伟华等[9]采用有效质量近似下的变分法研究了量子阱中极化子的声子平均数。然而,到目前为止,应用改进的线性组合算符和变分相结合的方法研究量子阱中束缚极化子性质的研究者[10,11]很少。本文采用采用改进的线性组合算符和变分相结合的方法研究了无限深量子阱中弱耦合束缚极化子的性质,并讨论了量子阱中束缚极化子的基态能量在不同的库仑束缚势 、电子-LO声子的耦合强度 、电子-LO声子的耦合强度 和阱宽d条件下随拉格朗日乘子u的变化关系。 和阱宽d条件下随拉格朗日乘子u的变化关系。
2 理论
考虑一个在 范围内无限高势垒的量子阱和 电子在 范围内无限高势垒的量子阱和 电子在 范围内充满极性半导体的量子阱中运动,并与极性半导体的LO声子场相互作用。选择平行于交界面的平面为x-y平面,阱心为原点。在理论推导中, 仅考虑了电子和LO声子的相互作用,忽略了IO声子的影响。利用Fr 范围内充满极性半导体的量子阱中运动,并与极性半导体的LO声子场相互作用。选择平行于交界面的平面为x-y平面,阱心为原点。在理论推导中, 仅考虑了电子和LO声子的相互作用,忽略了IO声子的影响。利用Fr hlich极化子理论[10], 将系统的哈密顿量[12]写成: hlich极化子理论[10], 将系统的哈密顿量[12]写成:
 (1) (1)
其中
 , , , , (2) (2)
 , (3) , (3)
 (4) (4)
其中 , , 分别为具有波矢 分别为具有波矢 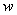 的声子的产生和湮灭算符, 的声子的产生和湮灭算符, 为 真空的介电常数。 为 真空的介电常数。 是电子的动量,系统的总动量 是电子的动量,系统的总动量 , ,  =( =( ,z)是电子的位置矢量,m为电子的带质量, ,z)是电子的位置矢量,m为电子的带质量, 是LO声子的频率, 是LO声子的频率,  由下式决定 由下式决定
 (5) (5)
 是半导体的体积, 其中无量纲耦合强度 是半导体的体积, 其中无量纲耦合强度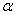 可以表示为: 可以表示为:
 (6) (6)
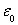 , ,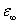 分别为半导体材料的静态和高频介电常数。 分别为半导体材料的静态和高频介电常数。
在绝热近似条件下,对电子的横向运动的动量和坐标引进改进的线性组合算符[13]

 ,(j=x,y ) (7) ,(j=x,y ) (7)

其中 是极化子的振动频率,取为变分参量, 是极化子的振动频率,取为变分参量,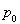 为 变分参量。 为 变分参量。
将式(2)中的库仑杂质势作级数展开[11]
 (8) (8)
对哈密顿量进行幺正变换
 (9) (9)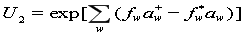 (10) (10)
则哈密顿量变为

 = = + + + +
+ + + + + - -
+ + + 
-
- - - (11) (11)
 (12) (12)
式(12)表示电子在反冲效应中发射和吸收不同波矢之间的相互作用而引起的附加能量,可以忽略。则该体系的哈密顿量的期待值为
  + + + + + +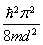
+ - - (13) (13)
对 变分得到 变分得到
 (14) (14)
对 变分得到 变分得到
 (15) (15)
将式(14)、(15)代入式(13),并用求和变积分的方法解得
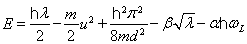 (16) (16)
其中 
由极值条件 ,可得 ,可得
 (17) (17)
将式(17)代入式(16),最后得到无限深量子阱中弱耦合束缚极化子的基态能量为
 (18) (18)
3 数值计算
采用改进的线性组合算符与变分相结合的方法研究了电子-LO声子在弱耦合情况下无限深量子阱中束缚极化子的基态能量 ,式(18)表明:无限深量子阱中强耦合极化子的基态能量 ,式(18)表明:无限深量子阱中强耦合极化子的基态能量 不仅与库仑束缚势 不仅与库仑束缚势 、电子-LO声子耦合强度 、电子-LO声子耦合强度 、阱宽d有关, 还和拉格朗日乘子 、阱宽d有关, 还和拉格朗日乘子 有关。为了更清楚说明它们之间的关系,通常取极化子单位( 有关。为了更清楚说明它们之间的关系,通常取极化子单位( ),以 ),以 为长度单位, 为长度单位, 为能量单位[14],通过数值计算。其结果表示为图1至图3。 为能量单位[14],通过数值计算。其结果表示为图1至图3。
1/2 1 2 下一页 尾页 |


