摘要：本文简单介绍了以 曲线为理论依据的塑性力学新方法【1】的基本原理，虽然新方法与经典方法相比具有不少优点，但是只有少数情况能求得解析解，大多情况还采用近似数值方法求解，基于这个原因，本文提出了新方法的有限元算法。
论文关键词：曲线,塑性力学新方法,有限元算法
1.以曲线为理论依据的塑性力学新方法简介
在塑性力学范围内，弹性力学建立的平衡方程、几何方程仍然适用，另外将应变 分为弹性应变 与塑性应变 两个部分，且弹性应变与应力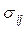 符合广义虎克定律，另一方面弹性应变与塑性应变之间总存在一定的函数关系，将上述思想用函数式表示出来，即得到弹塑性问题的统一基本方程组：
 （1）
上式中弹性应变与塑性应变关系式 而弹性应变与塑性应变之间的
关系是有规律可行的，具体包括以下两个方面：
1）简单加载情形，任意一条主应变的曲线(即弹性应变部分和塑性应变部分关系曲线)总可以由其它主应变的曲线沿弹性应变 轴平移而得到（如图1）。
图1
2）若取简单加载情形下的一条主应变曲线 作为基准线，则任
意应力应变状态下应变的弹性部分和塑性部分具有如下相关关系：
 （2）
式中  的含义如图1所示，式（2）考虑的是应变的绝对值。
2.塑性力学新方法的有限元算法
有限元方法求解塑性力学问题，其步骤与弹性力学问题介绍的步骤相同，为了便于分析，先考虑一个三角形单元的平面应力问题。
1）以单元结点位移作为基本未知量。设单元结点编码为 、 、 ，由于考虑的是平面问题，则每个结点在单元平面上有两个位移分量，整个单元将有六个结点位移分量，用列阵表示如下：
 （3）
式中  、 表示结点在 轴和 轴方向的位移。
选取适当的形函数 和位移模式，使单元内任一点的位移均可表示成单元结点位移的函数，
 （4）
2）单元力学特性
利用平面问题几何关系，可得到单元应变分量与结点位移的关系式
 （5）
得到应变后，再利用广义虎克定律，可求得单元应力。
3）单元刚度方程
根据虚位移原理，建立表征单元结点位移 与结点力 关系的刚度方程
 （6）
单元刚度矩阵的表达式为
 （7）
式（7）在塑性问题中是非线性的，采用割线刚度法求解。具体步骤如下：
a.首先不考虑塑性变形，按弹性状态计算，记此时的应变矩阵为 ，单元刚
度矩阵为 ，由式（6）可初步求出此时的单元结点位移记为 。
b.单元力学特性分析。由式（5）求出单元应变 ，这里认为单元应变包括弹性应变 与塑性应变 两部分。假定单元弹性应变与塑性应变之间存在如下关系：
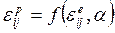
可得单元弹性应变与总应变之间总存在一定函数关系，写成关系式为
 （8）
则式（5）可改写成如下形式：
 （9）
式中  为考虑了塑性变形的应变矩阵
  （10）
求得 后，再由式（7）求得单元刚度矩阵记为 ，最后由式（6）求得单元结点位移记为 ，完成一次循环运算。
c.重复上一步的循环运算，直到 ，停止运算，得到较为满意的近似解。
3.结语
以曲线为基础的塑性力学新方法求解条理清楚,过程简洁,可以求解经典理论难以得到解析解的问题,具有较明显的优越性。本文以新方法为指导思想，提出了新方法的有限元算法，经算例验证，具有一定的可行性。
参考文献
1 李铀，白世伟，李锶等.以e-p 曲线为基础的塑性力学新方法的物理解释及应用实例[J].岩土工程学报. 2001，23(6)：704～707
|
