| 而且,当时域信号从一个瞬时的低功率波形传到一个高功率的信号时,大信号幅度的摆幅会相交,除非信号发射器的功率放大器在整个信号范围内显示出非常高的线形,否则将导致一个高的超出带宽的谐波失真,从而将会因相邻信道之间的干扰而导致信道传输质量的下降。
OFDM合成信号产生较大的峰值功率,由此带来较大的峰值平均功率比,简称峰均比。因此,OFDM系统内出现较大峰值功率信号的原因在于多个子载波信号的叠加。当N个资信号都以相同的相位求和时,所得到信号的峰值功率就会是平均功率的N倍,此时系带信号的峰值比为 ,如果N=256的话,OFDM系统的峰均比等于24dB,这是一种非常极端的情况,OFDM系统内的峰均比通常也不会达到这一数值。不过,对于未经过调制的载波来说,其峰均值为0。 ,如果N=256的话,OFDM系统的峰均比等于24dB,这是一种非常极端的情况,OFDM系统内的峰均比通常也不会达到这一数值。不过,对于未经过调制的载波来说,其峰均值为0。
要想通过降低峰均比改善OFDM的性能,首要任务需要选择理想的功率放大器。由于一般的功率放大器都不是线性的,而且其动态范围也是有限的,所以当OFDM系统内这种变化范围较大的信号通过非线性部件时,信号就会产生非线性失真,产生谐波,造成较明显的频谱扩展干扰以及带内信号畸变,导致整个系统性能的下降。当然了,虽然采用大动态范围的线性放大器能够对非线性放大器的工作点进行补偿,但是功率放大器的效率会大大降低,绝大部分能量都将转化为热能被浪费掉。这一方法并不适用所有系统。目前还可以采用信号预畸变技术和编码方法来减小峰均比从而提高OFDM系统性能。
三、用MATLAB对OFDM信号仿真的实现
1、OFDM信号的时域及频域波形
一个OFDM符号之内包含多个经过相移键控或者正交幅度调制的子载波。其中, 表示子载波的个数, 表示子载波的个数, 表示OFDM符号的持续时间(周期), 表示OFDM符号的持续时间(周期), ( ( )是分配给每个子信道的数据符号, )是分配给每个子信道的数据符号, 是第 是第 个子载波的载波频率, 个子载波的载波频率, ,则从 ,则从 开始的OFDM符号可以表示为: 开始的OFDM符号可以表示为:
 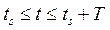 (1) (1)
 
其中s(t)的实部和虚部分别对应于OFDM符号的同相和正交分量,在实际中可以分别与相应子载波的cos分量和sin分量相乘,构成最终的子信道信号和合成的OFDM符号。在图4中给出了OFDM系统基本模型的框图,其中 。在接收端,将接收到的同相和正交矢量映射回数据消息,完成子载波解调。 。在接收端,将接收到的同相和正交矢量映射回数据消息,完成子载波解调。

图4:OFDM系统基本模型框图
OFDM信号的正交性还可以从频域角度来解释。根据式(1),每个OFDM符号在其周期 内包括多个非零的子载波。因此其频谱可以看作是周期为 内包括多个非零的子载波。因此其频谱可以看作是周期为 的矩形脉冲的频谱与一组位于各个子载波频率上的 的矩形脉冲的频谱与一组位于各个子载波频率上的 函数的卷积。矩形脉冲的频谱幅值为 函数的卷积。矩形脉冲的频谱幅值为 函数,这种函数的零点出现在频率为1/ 函数,这种函数的零点出现在频率为1/ 整数倍的位置上。图中给出了相互覆盖的各个子信道内经过矩形波形成型得到的符号的sinc函数频谱。在每个子载波频率最大值处,所有其他子信道的频谱值恰好为零。因为在对OFDM符号进行解调的过程中,需要计算这些点上所对应的每个子载波频率的最大值,所以可以从多个相互重叠的子信道符号中提取每一个子信道符号,而不会受到其他子信道的干扰。可以看出,OFDM符号频谱实际上可以满足奈奎斯特准则,即多个子信道频谱之间不存在相互干扰。因此这种一个子信道频谱出现最大值而其它子信道频谱为零点的特点可以避免载波间干扰(ICI)的出现。 整数倍的位置上。图中给出了相互覆盖的各个子信道内经过矩形波形成型得到的符号的sinc函数频谱。在每个子载波频率最大值处,所有其他子信道的频谱值恰好为零。因为在对OFDM符号进行解调的过程中,需要计算这些点上所对应的每个子载波频率的最大值,所以可以从多个相互重叠的子信道符号中提取每一个子信道符号,而不会受到其他子信道的干扰。可以看出,OFDM符号频谱实际上可以满足奈奎斯特准则,即多个子信道频谱之间不存在相互干扰。因此这种一个子信道频谱出现最大值而其它子信道频谱为零点的特点可以避免载波间干扰(ICI)的出现。
2、OFDM系统仿真实现
根据前面的OFDM系统模型框图,本论文利用Matlab语言编程实现OFDM系统。为了信号的有效传输,采用QPSK调制和解调方式,为了消除码间干扰和多径干扰造成的影响,还插入了保护间隔和循环编码。仿真了具有64个子载波,保护间隔为16点,每帧包含5个符号的OFDM系统。为了分析保护间隔和循环编码对系统误码性能的影响,在系统实现时特别设计了两种不同的方式,即带有保护间隔和循环编码的实现方式与无保护间隔的实现方式。进一步分析了在不同信道环境下系统的性能。信道包括高斯白噪声干扰与多径干扰两种情况。
(1)高斯白噪声环境下系统的性能

图5:高斯白噪声环境下采用QPSK调制解码前后的仿真曲线
图5中这两条曲线表示随着信噪比的增加,系统的误码率随之减小,这恰恰反映了通信系统有效性和可靠性的矛盾所在。在高斯白噪声环境下QPSK在信道解码前的误码率要高于信道解码后的误码率。这也恰恰说明了信道编码的优势所在。它不仅可以提高传输速率同时可以增加纠错能力。随着信噪比的增加,信道编解码的优势显现了出来,信道编解码后的误码率小于信道编解码前的误码率。
(2)多经干扰环境下系统的性能
图6中蓝色的曲线表示系统经过OFDM调制后在多径干扰下的误码性能,红色的曲线表示系统不经过OFDM调制情况下在多径干扰下的误码性能,可以看出,OFDM调制可以降低多径干扰带来的影响,使误码性能得到改善。 2/3 首页 上一页 1 2 3 下一页 尾页 |


