| 当接触变形ω足够小时, 粗糙峰发生弹性变形。由Hertz接触理论[1], 实际接触面积和平均接触压力与接触变形ω的关系被无量纲化后可分别表示为:
 (7) (7)
 (8) (8)
其中ωc,Pc,Ac分别为单一弹性球与刚性平面接触初始屈服点出现时的临界法向变形、临界载荷值及临界接触面积,并有如下公式[8]:
 (9) (9)
 (10) (10)
 (11) (11)
式中 Cv——为泊松比的函数,Cv=1.234+1.256v;
E——杨氏模量
Y——屈服强度
ρ——球形粗糙峰半径
v——泊松比
对于理想光滑球临界法向变形、临界载荷值、临界接触面积可表示为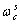 、 、 和 和 ,对于粗糙峰临界法向变形及临界载荷值可表示为 ,对于粗糙峰临界法向变形及临界载荷值可表示为 、 、 和 和 。 。
2.2 单一粗糙峰与刚性平面的弹塑性接触
当法向变形大于临界法向变形时ωc,弹性球会发生弹塑性接触,直到全塑性变形的发生。对于弹塑性变形阶段,经文献调研,目前尚未有任何精确解,一般是通过有限元等得出的经验公式等进行求解接触力学,本文将采用Kogut等[4]利用有限元得出的经验公式进行求解,其中接触载荷及接触面积与法向变形的关系可表示为:
 (12) (12)
 (13) (13)
2.3 单一粗糙峰与刚性平面的全塑性接触
Kogut等通过有限元分析计算得出,当法向变形大于110倍临界法向变形时,弹性球会完全处于全塑性状态,因此根据Abbott等[3]给出的理论,当弹性球与刚性平面处于全塑性接触的时候,接触力及接触面积和法向位移之间有如下关系式:
 (14) (14)
 (15) (15)
式中 H——为硬度值论文格式模板。
3 球形粗糙面与理想刚性面的接触模型
根据Greenwood等[2]的假设,粗糙峰之间没有相互作用,因此每个粗糙峰的法向接触力、接触面积只与其自身的变形量有关,Chang等推导出实际的法向接触力、接触面积的公式为:
 (16) (16)
 (17) (17)
而对于粗糙球与刚性平面的接触,Cohen等[10]给出了如下模型:
 (18) (18)
将式(7)代入到(18),得到只发生弹性变形的粗糙峰产生的总接触力为:
 (19) (19)
将式(19)通过在垂直和水平方向上归一化可以得到:
 (20) (20)
对于粗糙表面,Greenwood等引入了一个新的无量纲参数——塑性指数ψ,Cohen等[10]给出了如下关于屈服强度的表达式:
 (21) (21)
由式(9)和(21)可以得到:
 (22) (22)
由式(20)和(22)及弹性范围内 ,可得到无量纲化公式: ,可得到无量纲化公式:
 (23) (23)
同理,对于处于弹性、弹塑性及全塑性接触的粗糙峰所能承受的载荷可表示为:
 

 (24) (24)



 (25) (25)
其中式(24)和(25)中第一项表示处于弹性接触的粗糙峰,第二和第三项为弹塑性接触的粗糙峰,第四项为全塑性变形的粗糙峰。

图2 粗糙表面接触分析求解流程图
Fig. 2 Flowchart of contact analysis of rough surfaces
4 模型计算结果与讨论
4.1 模型求解方法及主要参数
式(24)中计算接触力与分离距离之间的函数关系采用了迭代的方法,因为对于球形面来说,在一定假定的初始载荷下,会使两接触表面产生一定的变形,部分靠近球顶面的粗糙峰被压平,计算初始的名义接触面积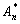 ,通过初始接触半径计算分离距离h,通过粗糙峰接触分离距离可计算新的接触力,而新的接触力会产生新的名义接触面积,以此类推,直到前后接触载荷的误差小于5%(设定的收敛准则)。具体计算流程见图2: ,通过初始接触半径计算分离距离h,通过粗糙峰接触分离距离可计算新的接触力,而新的接触力会产生新的名义接触面积,以此类推,直到前后接触载荷的误差小于5%(设定的收敛准则)。具体计算流程见图2:
球形粗糙表面接触主要形貌参数及材料性能参数见下表:
表1 球形粗糙接触模型表面形貌及材料性能参数
|
β
|
R/ρ
|
塑性指数 ψ
|
泊松比 ν
|
|
0.04
|
20
|
0.5, 2, 16
|
0.31
|
4.2 几种模型计算结果的比较与讨论
 

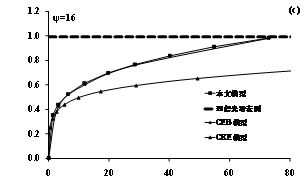
图3不同塑性指数条件下有效接触面积
与名义接触面积比率和无量纲载荷的关系
Fig.3 Effectivecontact area and normal contact area ratio vs. dimensionless load underdifferent plasticity index
图3所显示的是三种不同塑性指数ψ= 0.5、2及16条件下有效接触面积与名义接触面积的比率A0/An和无量纲载荷P/Pcs的函数关系。其中A0为实际有效接触面积,Pcs为理想光滑球基体在初始塑性变形产生时的临界接触载荷。CEB模型、CKE模型及理想光滑球接触模型也同时在图中绘出方便比较。理想光滑表面名义接触面积 可以通过如下得出[10]: 可以通过如下得出[10]:
 (26) (26)
从图中可以看出接触力学,对于较小载荷条件下,粗糙表面实际接触面积远小于名义接触面积(即相应理想光滑表面接触时),这是因为粗糙表面中部分粗糙峰处于弹塑性或全塑性接触,局部接触压力较大,因此,对于相同的接触载荷,实际有效接触面积比名义接触面积小。这与Greenwood 等提出的理论是完全相符的。在较低的塑性指数条件下,如ψ=0.5和2,本文模型与CKE模型符合很好,因为两个模型都考虑到粗糙峰不仅有弹性接触,还会有弹塑性接触,而由Greenwood等的预测,在此时,大部分粗糙峰处于弹塑性接触。而CEB模型因为未考虑粗糙峰的弹塑性接触阶段,认为粗糙峰一旦达到初始屈服点就会进入全塑性变形,而对于全塑性状态下,相同的接触载荷只会产生较小的接触面积,因此,CEB模型中部分粗糙峰已经处于全塑性状态,平均接触压力已达到极限值——硬度值,故相同载荷下CEB模型所预测的接触面积要比本文模型要小。而当塑性指数ψ= 16时,由Greenwood等的理论,基本上所有的粗糙峰都处于全塑性接触状态,而全塑性状态下的粗糙峰在相同载荷下都会有相同的接触面积,式(25)中第四项占据绝大部分,故与CEB模型的结果比较类似或者相同,而CKE模型因为没有考虑粗糙峰的全塑性变形,认为平均接触压力可以不断增大甚至超过极限值,因此接触力学,在相同载荷下,相反会得到较小的接触面积,但这是不科学的。
此外也能从图3中看出,随着塑性指数的增加,有效接触面积等于名义接触面积值时的无量纲临界载荷也在增加,即在塑性指数ψ= 0.5时的临界载荷大约为5,而对于塑性指数ψ= 16时的临界载荷增大到将近80。这是因为,对于大塑性指数条件下,粗糙峰的分布比较分散,其高斯分布均方差较大,要克服所有粗糙峰的影响需将所有粗糙峰压平,因而所需要的载荷相对较大。
2/3 首页 上一页 1 2 3 下一页 尾页 |


