论文导读::用Monte Carlo方法研究了外磁场中自旋-1与自旋-3/2混合三维Ising系统的磁性质。结果表明,系统磁矩随晶场的增强阶梯式减小,由于能量简并的解除,外磁场存在时磁矩随晶场变化的台阶数目增多。当单离子晶场 与 与 在同一台阶区域取值时,系统磁矩随外磁场的增强平缓地趋于饱和值,而当二者在不同台阶区域取值时,系统磁矩随外磁场的变化则表现出了较明显的台阶结构。单离子晶场 在同一台阶区域取值时,系统磁矩随外磁场的增强平缓地趋于饱和值,而当二者在不同台阶区域取值时,系统磁矩随外磁场的变化则表现出了较明显的台阶结构。单离子晶场 与 与 对于系统无序相的影响是不同的。 对于系统无序相的影响是不同的。
论文关键词:混合自旋,MonteCarlo,磁性质
1. 引言
近年来,人们对混合自旋系统产生了浓厚的兴趣并进行了初步研究。Y. Nakamura 等人[1]研究了自旋-1和自旋-3/2混合Ising铁磁系统的磁性质;A. Bobák[2,3]等人研究了各向异性晶场对二维正方晶格和二维蜂窝晶格混合自旋系统相变的影响;魏国柱等人[4]研究了简单立方晶格混合系统的相变问题。研究所采用的方法也各不相同,其中有有效场方法[2,3]、平均场方法[5,6]、集团变分法[7]等[8-10]。然而随着自旋 的增大和自旋的混合,会带来近似方法技术处理上的困难,而Monte Carlo模拟可以控制统计误差,准确处理自旋之间的相互作用,且不带有任何其他近似,因而是研究这类系统的有效方法。上面的研究仅仅考虑了交换相互作用和单离子晶场物理论文,而没有考虑对磁性系统有重要影响的外磁场的作用。本文用Monte Carlo方法研究考虑晶场与外磁场作用的自旋-1与自旋-3/2混合的简单立方晶格系统。结果表明,磁矩随晶场的增强而阶梯式减小,由于能量简并的解除,外磁场存在时台阶数目增多。当两单离子晶场在同一台阶区域取值时,系统磁矩随外磁场的增强平缓地趋于饱和值,而当二者在不同台阶区域取值时,系统磁矩随外磁场的变化则表现出了较明显的台阶结构。两单离子晶场对系统无序相的影响不同论文开题报告。 的增大和自旋的混合,会带来近似方法技术处理上的困难,而Monte Carlo模拟可以控制统计误差,准确处理自旋之间的相互作用,且不带有任何其他近似,因而是研究这类系统的有效方法。上面的研究仅仅考虑了交换相互作用和单离子晶场物理论文,而没有考虑对磁性系统有重要影响的外磁场的作用。本文用Monte Carlo方法研究考虑晶场与外磁场作用的自旋-1与自旋-3/2混合的简单立方晶格系统。结果表明,磁矩随晶场的增强而阶梯式减小,由于能量简并的解除,外磁场存在时台阶数目增多。当两单离子晶场在同一台阶区域取值时,系统磁矩随外磁场的增强平缓地趋于饱和值,而当二者在不同台阶区域取值时,系统磁矩随外磁场的变化则表现出了较明显的台阶结构。两单离子晶场对系统无序相的影响不同论文开题报告。
2. 模型与计算
模型哈密顿量
 .(1) .(1)
其中,自旋 , , ;第一项对最近邻求和, ;第一项对最近邻求和, ( ( )为最近邻格点间交换耦合常数, )为最近邻格点间交换耦合常数, 、 、 分别表示离子A、离子B处的晶场, 分别表示离子A、离子B处的晶场, 为外磁场。 为外磁场。
计算中,采用翻转单个自旋的Metropolis算法,取 的简单立方晶格系统,采用周期性边界条件。起初的10000MCS作为系统趋于平衡所需要的步数,不进行统计平均物理论文,而对以后的50000MCS所测量的物理量进行统计平均。 的简单立方晶格系统,采用周期性边界条件。起初的10000MCS作为系统趋于平衡所需要的步数,不进行统计平均物理论文,而对以后的50000MCS所测量的物理量进行统计平均。
系统的磁化强度
 ,(2) ,(2)
磁化率
 ,(3) ,(3)
每个格点的内能
 ,(4) ,(4)
比热
 ,(5) ,(5)
其中 为约化温度, 为约化温度,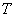 是绝对温度, 是绝对温度, 为玻尔兹曼常数。 为玻尔兹曼常数。
3. 结果与讨论
图1 给出了磁矩随晶场的变化关系。为确定起见,取定温度 ,外磁场分别取 ,外磁场分别取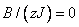 和 和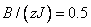 ( ( 为配位数)。 为配位数)。

图1 磁矩 随晶场 随晶场 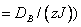 的变化 的变化
可以看出,不论外磁场存在与否,磁矩随晶场   的增大阶梯式降低,这与Y. Nakamura等人[1]的结果一致。当晶场取不同范围内的值时,系统处于不同的台阶。无外磁场时,三个台阶分别位于 的增大阶梯式降低,这与Y. Nakamura等人[1]的结果一致。当晶场取不同范围内的值时,系统处于不同的台阶。无外磁场时,三个台阶分别位于 、 、 和 和 区,相应的磁矩分别为1.0,0.3和0。当存在外磁场时,磁矩随晶场变化的台阶数目由3个变为4个,即系统的有序相增多,这与外磁场中系统能量简并的解除有关。 区,相应的磁矩分别为1.0,0.3和0。当存在外磁场时,磁矩随晶场变化的台阶数目由3个变为4个,即系统的有序相增多,这与外磁场中系统能量简并的解除有关。
图2给出了不同参数条件下系统磁矩随温度的变化关系。其中实线表示无外磁场时, 分别取0、0.33、0.33和0.33, 分别取0、0.33、0.33和0.33, 分别取0、0.33、0.40和0.65时的结果;虚线是对应的外磁场 分别取0、0.33、0.40和0.65时的结果;虚线是对应的外磁场 取0.5时的结果。计算表明物理论文,在无外磁场的情况下,若 取0.5时的结果。计算表明物理论文,在无外磁场的情况下,若  ,系统从有序相到无序相的转变温度 ,系统从有序相到无序相的转变温度 约为 约为

图2磁矩 随温度 随温度 的变化 的变化
3.71;当   时,相变温度 时,相变温度 约为1.76;当 约为1.76;当 , ,  时,相变温度 时,相变温度 约为1.41;当 约为1.41;当 , ,  时,相变温度 时,相变温度 约为0.81,即晶场的增强可以使系统更快地从有序相转变到无序相。低温下, 约为0.81,即晶场的增强可以使系统更快地从有序相转变到无序相。低温下,  与 与 取在同一台阶区域(曲线1 取在同一台阶区域(曲线1   、曲线2 、曲线2   、曲线3 、曲线3  , , )时,对应的有序相是相同的; )时,对应的有序相是相同的; 与 与 取在不同台阶区域(曲线4 取在不同台阶区域(曲线4  , , )时,对应的则是另一有序相。与无外磁场时的对应情况相比,当有外磁场存在时,系统的磁矩在不同的温度区域有不同程度的增大,磁矩随温度升高而降低的速度趋缓,系统从有序相到无序相的转变温度更高。 )时,对应的则是另一有序相。与无外磁场时的对应情况相比,当有外磁场存在时,系统的磁矩在不同的温度区域有不同程度的增大,磁矩随温度升高而降低的速度趋缓,系统从有序相到无序相的转变温度更高。
1/2 1 2 下一页 尾页 |


