那么, 的分布函数属于 的分布函数属于 ; ;
假设当 时成立,即 时成立,即 的分布函数属于 的分布函数属于 。那么,当 。那么,当 时,假设 时,假设 的分布函数 的分布函数 属于 属于 , , 则 则


同理可得
 , ,
命题得证。
引理3  和 和 是相互独立的非负的随机变量,分布函数分别为 是相互独立的非负的随机变量,分布函数分别为 。 。 有界但在0点是非退化的。 有界但在0点是非退化的。 ,则 ,则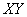 的分布函数仍然属于 的分布函数仍然属于 。 。
有关证明可参阅参考文献[1]。
3.定理及证明
定理1 令 ,则(1.1)定义的盈余模型的破产概率 ,则(1.1)定义的盈余模型的破产概率
 .(3.1) .(3.1)
证明:考虑当前的盈余额 ,则由(1.1)有 ,则由(1.1)有
 (3.2) (3.2)
则所求的破产概率转化为
 (3.3) (3.3)
根据(3.2),有

(3.3)可写为
 (3.4) (3.4)
根据负相协的性质可知: 是负相协的随机变量序列。 是负相协的随机变量序列。
如果我们证明了:
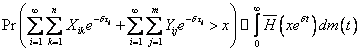 (3.5) (3.5)
对于任意的 ,有 ,有

根据引理3可知 ,据(2.1)式和 ,据(2.1)式和 的任意性有: 的任意性有:
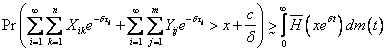 (3.6) (3.6)
根据(3.4)、(3.5)、(3.6)可知:要证明定理1成立,只需证明(3.5)成立即可,
下面我们证明(3.5)成立。
令
 , ,
根据引理1和引理2可知: 的分布函数 的分布函数 仍然在重尾分布族 仍然在重尾分布族 中, 中,
根据参考文献[1],对于变量 存在有限的正整数 存在有限的正整数 和 和 ,当 ,当 , ,
 (3.7) (3.7)
对于任意的 ,有 ,有


  (3.8) (3.8)
根据(3.7)和(3.8),由 的任意性,我们显然可得 的任意性,我们显然可得

由
 , ,  , ,
有
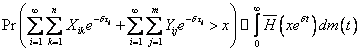
(3.5)式成立
命题得证。
4.结论
在巨额索赔服从重尾分布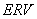 族的条件下,我们得到了风险模型的破产概率: 族的条件下,我们得到了风险模型的破产概率:
 . .
由得到的破产概率计算公式,可知:承保巨灾风险和小额保单的保险公司,小额保单对保险公司债务风险的影响较小,它承保的巨灾风险是决定保险公司出现债务危机的关键因素。
参考文献
[1]YiqingChen,Kai W.Ng. The ruin probability of the renewal model with constant interestforce and negatively dependent heavy-tailed claims[J]. Insurance: Mathematicsand Economics, 2007, 40: 415-423.
[2]Embrechts.P.,Goldie.C., Mikosch.T., Modelling Extremal Events for Insurance and Finance [M]. Berlin: Springer, 1997.
[3]Rob Kass,Qihe Tang. A large deviation result for aggregate claims with dependent claimoccurrences[J]. Insurance: Mathematics and Economics, 2005, 36: 251-259.
[4]SheldonM.Ross.Introduction to Probablity Models[M].Singapore:Elsevier Pte Ltd,2007.
[5]Bingham, N.H., Goldie, C.M., Teugels,J.L., 1987. Regular Variation.Cambridge University Press, Cambridge.
[6]高珊,孙道德.重尾索赔下的一类相依风险模型的若干问题[J].经济数学,2007,24(2):111-115.
[7]Tang, Q.,2005b. The finite-time ruin probability of the compound Poisson model withconstant interest force. Journal of Applied Probability 42(3), 608–619.
[8]Tang, Q.,Tsitsiashvili, G., 2003. Precise estimates for the ruin probability in finitehorizon in a discrete-time model with heavy-tailed insurance and financialrisks. Stochastic Processes and their Applications 108 (2), 299–325.
[9]Tang, Q.,Tsitsiashvili, G., 2004. Finite- and infinite-time ruin probabilities in thepresence of stochastic returns on investments. Advances in Applied Probability36 (4), 1278–1299.
[10]Tang,Q., 2005a. Asymptotic ruin probabilities of the renewal model with constant interest force and regular variation. Scandinavian Actuarial Journal (1), 1–5.
2/2 首页 上一页 1 2 |


