论文导读::根据保险公司的实际情况:在同一时刻会出现多种类型的索赔,而且同种类型的索赔都存在弱相关性。构建了一个多种轻尾索赔和多种重尾索赔同时发生且同类型索赔存在负相协关系的风险模型。根据
论文关键词:
1.建立模型
我们建立的风险模型,主要解决的是既承保巨灾风险又承保小额保险的保险公司债务风险的破产概率,研究的是保险公司在同一时刻既有小额索赔又有巨额索赔的情况。保险公司承保能力是有限度的,同类型的索赔中,某一个理赔额较大,那其他的理赔额额必然会减少。所以,假设同类型索赔之间服从负相协的关系。
建立一个索赔额模型如下:

其中,负相协同分布随机变量序列 (其中 (其中 为有限自然数)具有分布 为有限自然数)具有分布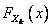 和一阶矩 和一阶矩 且 且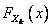 服从重尾分布。负相协同分布随机变量序列 服从重尾分布。负相协同分布随机变量序列 (其中 (其中 为有限自然数)具有共同分布 为有限自然数)具有共同分布 和有限一阶矩 和有限一阶矩 且 且 服从轻尾分布。 服从轻尾分布。
我们假设: 和 和 对应的索赔发生时间相同。 对应的索赔发生时间相同。 该式对所有的 该式对所有的 都成立。 都成立。
每个索赔的到达时间 是一列非负的独立同分布随机变量,两次索赔之间的时间间隔 是一列非负的独立同分布随机变量,两次索赔之间的时间间隔 也构成一个非负的独立同分布随机变量序列。 也构成一个非负的独立同分布随机变量序列。
令 ,假设在时间 ,假设在时间 内发生的索赔个数为 内发生的索赔个数为 , , 的期望为 的期望为 ,则 ,则

建立盈余模型:

该式可转化为
 (1.1) (1.1)
其中,初始盈余为 ,利息为常数 ,利息为常数 ,保费率为常数 ,保费率为常数 , , 是示性函数。破产概率定义为: 是示性函数。破产概率定义为:

2.基本知识及引理
本文的破产概率主要在重尾分布子族 下研究。 下研究。
分布族 中的任意分布函数 中的任意分布函数 满足:对任意的 满足:对任意的 ,有 ,有
 ,(2.1) ,(2.1)
其中 . .
一列负相协的随机变量序列 满足:对 满足:对 的任意两个非空、不交子集 的任意两个非空、不交子集 , , 以及任意两个单调不降的函数 以及任意两个单调不降的函数 和 和 ,不等式 ,不等式

成立,其中涉及的矩存在。
引理1相互独立的非负随机变量序列 (其中 (其中 )分布函数分别为 )分布函数分别为 , , ,令 ,令
 , , 。 。
则 的分布函数属于重尾子族 的分布函数属于重尾子族 。 。
有关证明可参阅参考文献[2]。
引理2  和 和 是相互独立的非负随机变量,分布函数分别为 是相互独立的非负随机变量,分布函数分别为 和 和 , ,  ,则 ,则 ( ( 为有限自然数)的分布函数仍然属于 为有限自然数)的分布函数仍然属于 。 。
证明:
由积分中值定理及 分布族的性质可知: 分布族的性质可知:
当 时,假设 时,假设 ,有 ,有


同理可得
 , ,
1/2 1 2 下一页 尾页 |


