| 在式(12)~式(16)中
 (17) (17)
 (18) (18)
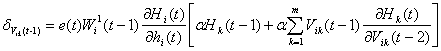 (19) (19)
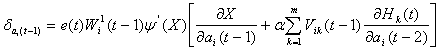 (20) (20)
 (21) (21)
其中式(20)和式(21)中 为: 为:
 (22) (22)
 、 、 可由 可由 得到。 得到。
在(18)至(21)中可知, 时刻的偏导数依赖于 时刻的偏导数依赖于 时刻的偏导数小论文。在Elman小波神经网络的训练开始时,给定一个初始值数学建模论文,令 时刻的偏导数小论文。在Elman小波神经网络的训练开始时,给定一个初始值数学建模论文,令
 , , , , , , , ,
在网络的训练过程中,如果学习速率过小,则网络的收敛速度较慢,如果学习速率过大,则在网络训练将发生振荡,甚至导致网络无法收敛,所以本文采用自适应动态学习速率 进行网络的训练,其学习速率 进行网络的训练,其学习速率 按式(23)进行变化。 按式(23)进行变化。
 (23) (23)
式中: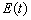 ―表示 ―表示 时刻的网络误差; 时刻的网络误差; ―表示 ―表示 时刻的学习速率; 时刻的学习速率; 为一为常数,通常取值为0.01~0.03之间。 为一为常数,通常取值为0.01~0.03之间。
(4)终止条件
按步骤(3)进行网络参数的不断调整数学建模论文,直到网络训练的误差达到给定的精度或最大训练次数,则终止网络训练,输出预测结果。
2.Elman小波神经网络在挠力河流域地下水开采量预测
(1)基本资料
1988~2007年挠力河流域地下水开采量如表1所示[9],从表1可以看出,在2000年地下水开采量减幅较大,主要由于在该年缩减了部分水田面积,但随着近年来水田的面积的增加,地下水开采量也呈现了明显增加的趋势。
表1挠力河流域地下水开采量统计表
Table 1 The exploitationstatistics of groundwater in Naoli river basin 单位:104m3
|
年份
|
1988
|
1989
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
1996
|
1997
|
|
开采量
|
9354
|
15306
|
18079
|
19023
|
15289
|
20456
|
14429
|
17195
|
43166
|
66458
|
|
年份
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
|
开采量
|
80601
|
92210
|
75474
|
90933
|
98258
|
101854
|
128354
|
135105
|
139571
|
142827
|
(2)样本的确定
由于地下水开采量的变化属于单因素时间序列,须先进行数据分析,确定输入输出样本对。本文采用了相关分析技术求解自相关函数,结果达到显著水平,各年地下水开采量与前1、3、4年的地下水开采量有关。为了计算方便,现取前4年的地下水开采量作为Elman小波神经网络的输入数学建模论文,本年的地下水开采量作为Elman小波神经网络的输出小论文。由此将1988~2006年的19个数据作为样本的输入,将2007年数据作为网络检验样本,则生成样本对共计16对,用这些数据对Elman小波神经网络模型进行训练与学习。
(3)网络结构的确定
根据输入样本的前4年地下水开采量作为网络的输入,则网络输入层神经元的个数为4,输出层神经元的个数为1,当隐含层神经元个数为2,关联层神经元个数为2,当训练次数为5758次时,网络收敛,误差精度达到0.01,拟合程度较好,故此网络结构为4-2-2-1。
(4) 结果分析
采用Elman小波神经网络对挠力河流域1992-2006年地下水开采量进行拟合数学建模论文,并对2007年地下水开采量进行检验,其拟合效果如图2和表2所示。从图2上可以看出所建立的模型拟合趋势和原历史数据基本一致,从表2可以得出拟合平均相对误差为3.10%,检验的相对误差为0.83%,模型的精度较高,在误差允许的范围之内,可以采用该模型对未来地下水开采量进行预测。

图2 1992-2007年挠力河地下水开采量观测值和拟合值的拟合图
Fig.2The fitting graph of groundwater exploitation observation value andfitting value in Naohe basin from 1992 to 2007
表2 1992-2007年挠力河流域地下水开采量拟合情况表
|
年份
|
观测值
|
预测值
|
相对误差(%)
|
年份
|
观测值
|
预测值
|
相对误差(%)
|
|
1992
|
15289
|
16720
|
9.36
|
2000
|
75474
|
76170
|
0.92
|
|
1993
|
20456
|
20080
|
1.84
|
2001
|
90933
|
92119
|
1.30
|
|
1994
|
14429
|
14859
|
2.98
|
2002
|
98258
|
98316
|
0.06
|
|
1995
|
17195
|
16335
|
5.00
|
2003
|
101854
|
101508
|
0.34
|
|
1996
|
43166
|
41105
|
4.77
|
2004
|
128354
|
124564
|
2.95
|
|
1997
|
66458
|
60458
|
9.03
|
2005
|
135105
|
138712
|
2.67
|
|
1998
|
80601
|
83033
|
3.02
|
2006
|
139571
|
140223
|
0.47
|
|
1999
|
92210
|
90623
|
1.72
|
2007
|
142827
|
141636
|
0.83
|
The fitting graph of groundwater exploitation in Naohe basin from 1992 to2007
table2 采用以上建立了地下水开采量Elman小波神经网络预测模型对2008-2013年挠力河流域地下水开采量进行预测,其预测结果如表3所示,从表3中可以看出,地下水开采量整体趋势是不断增加的,平均年增加幅度为0.89%。
表3 三江平原挠力河流域地下水开采量
|
年份
|
开采量(104m3)
|
增幅(%)
|
年份
|
开采量(104m3)
|
增幅(%)
|
|
2008
|
143481.75
|
0.46
|
2011
|
148334.55
|
2.84
|
|
2009
|
142526.44
|
-0.67
|
2012
|
149768.31
|
0.97
|
|
2010
|
144232.33
|
1.20
|
2013
|
150551.29
|
0.52
|
The groundwater exploitation of Naoli river basin in Sanjiang plain
table33.结论
本文在Elman神经网络和小波理论的研究基础上,将小波理论与Elman神经网络进行耦合建立了Elman小波神经网络模型,同时给出了网络的训练过程数学建模论文,为了提高网络的训练速度,本文在网络的训练过程中,采用了自适应学习速率进行网络训练。最后,将该模型应用到挠力河流域地下水开采量预测,建立了挠力河流域地下水开采量预测模型,从拟合和预测结果中可以看出,证明建立的挠力河流域地下水开采量的Elman小波神经网络模型是可行的,同时证明该模型具有较强的逼近和容错能力、较快的收敛速度和较好的预报效果,为制定挠力河流域水资源规划和政府部门提供理论参考,同时可以应用到其它区域地下水开采量的预报中。
参考文献
1.刘正茂,夏广亮,赵艳波.三江平原地下水生态开采对生态过程的影响[J].水利发展研究, 2006,(12):38-41
2.吴昌友.三江平原地下水数值模拟及仿真问题研究[D].东北农业大学博士论文,2009,103-113
3.李勤奋,方正,王寒梅.上海市地下水可开采量模型计算及预测[J].2000,62(2):36-43
4.Elman J L. Finding structure in time[J].Cognitive Science (S0364-0213),1990, (14):179-211
5.Wen Yu. Nonlinear system identification using discrete-time recurrentneural networks with stable learning algorithms[J]. Information Sciences (S0020-0255),2004, (158):131-147
6.巫庆辉,邵诚.基于递归型小波神经网络的感应电动机伺服驱动系统自适应控制[J].机械工程学报,2005,41(2):71-76
7.赵凤遥,马震岳.基于递归小波神经网络的非线性动态系统仿真.系统仿真学报[J],2007,19(17):1453-1456
8.付强.农业水土资源系统分析与综合评价[M].北京:中国水利水电出版社,2005,126-128
9.黑龙江省水利水电勘测设计研究院.三江平原水利综合规划―地下水资源调查评价报告[R], 2007
2/2 首页 上一页 1 2 |


