
那么,K满足约束条件

设u为第k阶段各项备件库存增量,且u={u,u,……,u},其中
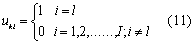
上式表示第k阶段第l项备件库存数增加1件,则状态转移方程为

设r为第k阶段第l项备件的边际效能,△为每个阶段参与比较的第i项备件的边际效能,则

令f(x)表示第k阶段各项备件的短缺数之和,则最优递推方程为

此时,

求解式(14)的关键是确定各阶段的边际效能r,方法是:在每个阶段依次将各备件的边际效能△进行比较,其值最大的备件即为第l项备件,该备件的边际效能即为r,这一阶段就选择该备件作为库存——其库存增加1件;用该备件库存再增加1件时产生的边际效能参与下一阶段的比较,参与比较的其他备件的边际效能不变。
5算例
某基地库存总保障经费为40万元,其备件库存的统计数据如表1所示。
表1某基地备件库存情况的统计数据
|
项号(i)
|
年平均需求(m)
|
平均修理时间(T)
|
供应渠道平均数(mT)
|
单价(¥10000)
|
|
1
|
10
|
0.1
|
1
|
5
|
|
2
|
50
|
0.08
|
4
|
1
|
|
3
|
5
|
0.2
|
1
|
8
|
首先,根据式(4)、(5)求出各项备件不同库存量的短缺数,再根据式(8)求出各备件的边际效能。令总库存量s=0,1,2,……,14(s的取值要使各项备件的短缺数均达到极小或0,以满足用边际分析法计算的需要),则各项备件的短缺数和边际效能如表2所示。
表2某基地各项备件的短缺数和边际效能
|
总库存量(s)
|
EBO
(s )
|
△
|
EBO
(s )
|
△
|
EBO (s )
|
△
|
|
0
|
1
|
|
4
|
|
1
|
|
|
1
|
0.3679
|
0.1264
|
3.0183
|
0.9817
|
0.3679
|
0.0790
|
|
2
|
0.1036
|
0.0528
|
2.1099
|
0.9084
|
0.1036
|
0.0330
|
|
3
|
0.0233
|
0.0161
|
1.3480
|
0.7619
|
0.0233
|
0.0100
|
|
4
|
0.0043
|
0.0038
|
0.7815
|
0.5665
|
0.0043
|
0.0024
|
|
5
|
0.0007
|
0.0007
|
0.4103
|
0.3712
|
0.0007
|
0.0005
|
|
6
|
0.0001
|
0.0001
|
0.1954
|
0.2149
|
0.0001
|
0.0001
|
|
7
|
0.0000
|
0.0000
|
0.0848
|
0.1107
|
0.0000
|
0.0000
|
|
8
|
0.0000
|
0.0000
|
0.0336
|
0.0511
|
0.0000
|
0.0000
|
|
9
|
0.0000
|
0.0000
|
0.0123
|
0.0214
|
0.0000
|
0.0000
|
|
10
|
0.0000
|
0.0000
|
0.0041
|
0.0081
|
0.0000
|
0.0000
|
|
11
|
0.0000
|
0.0000
|
0.0013
|
0.0028
|
0.0000
|
0.0000
|
|
12
|
0.0000
|
0.0000
|
0.0004
|
0.0009
|
0.0000
|
0.0000
|
|
13
|
0.0000
|
0.0000
|
0.0001
|
0.0003
|
0.0000
|
0.0000
|
|
14
|
0.0000
|
0.0000
|
0.0000
|
0.0001
|
0.0000
|
0.0000
|
然后,根据式(7)以及(9)~(15),用Matlab编写计算程序,并求出各项备件的最优库存和总短缺数。计算结果:最优库存为(3,9,2),总短缺数为0.1392。
最后,根据式(3)计算供应可用度。已知该基地机群飞机架数为24,为同一种机型,各项备件的单机安装数为(1,2,1),则其供应可用度为99.42%。
6结论
(1)以上是从装备系统的效能出发考虑其备件库存,不仅为决策层(即装备主管)要达成的装备可用度标准提供了保证,而且使可用度所需的费用最小(如果是其他库存配套方案,要达到同样的可用度都会使费用增加)。
(2)用边际分析法编写的算法便于计算机实现,而且边际分析法不仅可以求出某些给定经费下的最优库存,还可以得到中间过程中不同经费下的库存储备方案(如表3所示),这对库存决策具有良好的参考价值。
表3某基地各项备件不同费用下的库存量与短缺数
|
总库存量(s)
|
库存量(s )
|
库存量(s )
|
库存量(s )
|
总短缺数(z)
|
总费用
|
|
1
|
0
|
1
|
0
|
5.0183
|
1
|
|
2
|
0
|
2
|
0
|
4.1099
|
2
|
|
3
|
0
|
3
|
0
|
3.3480
|
3
|
|
4
|
0
|
4
|
0
|
2.7815
|
4
|
|
5
|
0
|
5
|
0
|
2.4103
|
5
|
|
6
|
0
|
6
|
0
|
2.1954
|
6
|
|
7
|
1
|
6
|
0
|
1.5633
|
11
|
|
8
|
1
|
7
|
0
|
1.4526
|
12
|
|
9
|
1
|
7
|
1
|
0.8205
|
20
|
|
10
|
2
|
7
|
1
|
0.5563
|
25
|
|
11
|
2
|
8
|
1
|
0.5051
|
26
|
|
12
|
2
|
8
|
2
|
0.2409
|
34
|
|
13
|
2
|
9
|
2
|
0.2195
|
35
|
|
14
|
3
|
9
|
2
|
0.1392
|
40
|
边际分析法的不足之处是它不能够求出所有整数费用值下的最优解,其迭代过程中每一步的步长由备件单价决定。但是,对备件保障人员来说,要保障的备件成千上万,使用边际分析法足以得出全部有实用价值的解,求出针对所有整数费用值的解完全没有必要。
实验结果表明该模型及其算法对实际应用具有很好的指导性意义。
参考文献
1 王效安. 航材仓库管理学[M]. 北京: 国防工业出版社, 2001: 89-94.
2 张衡, 花兴来, 许绍木. 可修复备件系统库存决策仿真优化模型[J].系统工程与电子技术, 2009, 31(6):1510-1514.
3 Craig C, Sherbrooke. 装备备件最优库存建模:多级技术[M]. 第二版. 贺步杰, 译. 北京: 电子工业出版社, 2008:19-22.
4 陆四海, 郑金忠, 季鸣. 基于ARINC模型的航材保障效能指标分析[J]. 仓储管理与技术, 2007(4):29-31.
5 郑金忠, 陆四海, 李友虎. 基于效用函数的航材保障效能评估[J].物流技术, 2007, 26(8):246-248.
6 曹文静, 徐廷学. 军械器材管理[M]. 烟台: 海军航空工程学院出版社, 2009:130-140.
7 王海霞, 汤文成, 钟秉林. 零部件最优库存量控制的研究[J].系统工程学报, 2000, 15(3):299-304.
8 罗兵, 胡啟军, 尹迪. 基于边际分析法确定备件补给数量[J].物流技术, 2009, 28(10):146-148.
9 张瑞昌, 赵嵩正. 航材保障经费的优化配置研究[J]. 北京航空航天大学学报, 2005, 31(1):102-104.
10 U Dinesh Kumar. 可靠性、维修与后勤保障:寿命周期方法[M]. 刘庆华, 宋宁哲, 译. 北京: 电子工业出版社, 2010:177-180. 2/2 首页 上一页 1 2 |


