
模型中 为因变量,表示上市公司的市场占有率。 为因变量,表示上市公司的市场占有率。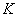 和 和 为解释变量,分别表示上市公司的研发经费支出和技术人员数, 为解释变量,分别表示上市公司的研发经费支出和技术人员数, 和 和 为控制变量,分别表示上市公司的资产规模和销售费用, 为控制变量,分别表示上市公司的资产规模和销售费用, 是回归方程的截距项, 是回归方程的截距项, 是回归方程的残差项。 是回归方程的残差项。
(五)R&D投入与市场占有率的相关性检验
首先我们利用2007~2009年三年的数据,采用普通最小二乘法,通过SPSS16.0软件处理,得到结果如表1、2、3三张表:
表1引入/剔除的变量a
|
模型
|
进入变量
|
剔除变量
|
方法
|
|
1
|
M
|
K,L,SIZE
|
逐步回归(标准:F的可能性≤0.05的变量进入,
F的可能性≥0.10的变量剔除)
|
|
2
|
K
|
L,SIZE
|
逐步回归(标准:F的可能性≤0.05的变量进入,
F的可能性≥0.10的变量剔除)
|
|
3
|
SIZE
|
L
|
逐步回归(标准:F的可能性≤0.05的变量进入,
F的可能性≥0.10的变量剔除)
|
|
a. 因变量:SHARE
|
|
表2 模型摘要
|
模型
|
R
|
R2
|
Adjusted R2
|
误差估计
|
D-W
|
|
1
|
0.789a
|
0.623
|
0.618
|
0.178573736
|
|
|
2
|
0.860b
|
0.740
|
0.734
|
0.149062052
|
|
|
3
|
0.883c
|
0.779
|
0.771
|
0.138321314
|
1.921
|
|
a. 预测因子: (常量), M
|
|
|
|
b. 预测因子: (常量), M, K
|
|
|
|
c. 预测因子: (常量), M, K, SIZE
|
|
|
|
d. 因变量: SHARE
|
|
|
表3系数a
|
模型
|
非标准的回归系数
|
标准的回归系数
|
t
|
Sig.
|
VIF
|
|
B
|
标准误差
|
Beta
|
|
1
|
(常量)
|
0.114
|
0.027
|
|
4.158
|
0.000
|
|
|
M
|
8.929E-6
|
0.000
|
0.789
|
11.632
|
0.000
|
1.000
1.000
|
|
2
|
(常量)
|
0.077
|
0.024
|
|
3.259
|
0.002
|
|
|
M
|
6.195E-6
|
0.000
|
0.547
|
7.903
|
0.000
|
1.496
1.496
|
|
K
|
5.076E-5
|
0.000
|
0.420
|
6.057
|
0.000
|
1.496
1.496
|
|
3
|
(常量)
|
0.048
|
0.023
|
|
2.075
|
0.041
|
|
|
M
|
4.650E-6
|
0.000
|
0.411
|
5.564
|
0.000
|
1.976
1.976
|
|
K
|
3.798E-5
|
0.000
|
0.314
|
4.473
|
0.000
|
1.784
1.784
|
|
SIZE
|
3.654E-7
|
0.000
|
0.292
|
3.751
|
0.000
|
2.194
2.194
|
|
a. 因变量:SHARE
|
表1显示了逐步回归的过程,按照对市场占有率的影响贡献程度的大小,逐个引入通过0.05显著性水平检验的三个解释变量,即销售费用、R&D费用和企业规模,从而建立了三个模型,剔除了未通过显著性检验的解释变量技术人员数中国论文下载中心。由表2可知,三个模型的Adjusted R2分别为0.618、0.734和0.771企业管理论文,显示了随着三个解释变量的引入,修正后的可决系数呈现明显增大趋势,即拟合优度变化显著。当解释变量增加到销售费用、R&D费用和企业规模三个变量时,方程的拟合程度最高。最优模型即第三个模型的D-W值(杜宾-瓦森检验值)为1.921,接近于2,可以认为该方程的残差不相关。表3显示了三个模型的回归系数、常数及t检验结果,可见,销售费用、研发费用和企业规模都通过了5%显著性水平检验,并且回归系数均为正,所以可以认为市场占有率与销售费用、R&D费用、企业规模之间存在正相关关系。第三个模型中三个自变量的VIF(方差膨胀因子)的值均在10以内,说明自变量为销售费用、研发费用和企业规模,因变量为市场占有率的模型中不存在严重的多重共线性。
由于截面数据中可能存在异方差,导致回归参数估计量不再有效,所以本文利用上步回归得到的普通残差的绝对值和市场占有率进行Spearman等级相关系数来检验是否存在异方差。如表4,结果表明普通残差的绝对值和市场占有率的Spearman等级相关系数为0.208,p值为0.057,略大于0.05,表明有可能存在异方差。
表4Spearman相关系数
|
|
|
SHARE
|
w
|
|
SHARE
|
相关系数
|
1.000
|
0.208
|
|
Sig. (2-tailed)
|
.
|
0.057
|
|
N
|
84
|
84
|
|
w
|
相关系数
|
0.208
|
1.000
|
|
Sig. (2-tailed)
|
0.057
|
.
|
|
N
|
84
|
84
|
为了消除异方差对模型估计造成的影响,本文用加权最小二乘法对原模型进行修正,权重为此前普通最小二乘法回归得到的普通残差绝对值的倒数,再次回归得到结果如表5:
表5加权最小二乘估计结果
|
SHARE
|
|
|
回归系数
|
t值
|
Sig.
|
VIF
|
|
K
|
0.385
|
5.173
|
0.000
|
3.488
|
|
SIZE
|
0.191
|
11.222
|
0.000
|
1.596
|
|
M
|
0.510
|
8.214
|
0.000
|
3.555
|
|
Adj R2
|
0.972
|
|
F
|
961.176
|
|
D-W
|
1.881
|
可见,修正后模型的拟合优度得到了较大的改善。修正的判定系数从0.771上升为0.972,表明修正后的方程很好地拟合了样本的数据。方程的D-W值接近于2,可以认为该方程的残差项之间是不相关的。研发费用、企业规模和销售费用三个自变量VIF值均小于10,可认为不存在严重的多重共线性。三个自变量均通过了0.05显著性水平检验,并且回归系数均为正,表明R&D费用支出、企业规模和销售费用与市场占有率具有显著地相关性,且这种相关性是正向的。
为了检验是否已经消除异方差的影响企业管理论文,我们再次对修正后的模型的残差的绝对值与市场占有率进行Spearman等级相关系数检验,如表6:
表6Spearman相关系数
|
|
|
SHARE
|
w1
|
|
SHARE
|
相关系数
|
1.000
|
0.190
|
|
Sig. (2-tailed)
|
.
|
0.084
|
|
N
|
84
|
84
|
|
w1
|
相关系数
|
0.190
|
1.000
|
|
Sig. (2-tailed)
|
0.084
|
.
|
|
N
|
84
|
84
|
结果表明修正后模型的残差的绝对值与市场占有率的等级系数的p值从0.057上升到了0.084,显著性水平在一定程度上降低了,由此可以认为模型的异方差问题得到了一定程度的解决。
(六)简要的研究结论
线性回归分析得出结论:技术人员投入与市场占有率不具有显著的相关性,R&D费用支出、企业规模和销售费用与市场占有率具有显著地相关性,且这种相关性是正向的。
因此,医药生物企业应该更加主动,把技术创新放在战略首位,加大R&D费用的投入,保持企业可持续发展,使企业拥有持续的竞争力,扩大市场占有率,在同行业中处于有利的竞争地位。虽然本研究表明,企业科技人员数与市场占有率不显著相关,但是医药生物行业的高科技性质决定了其对人才需求之高,高素质人才影响着企业的核心竞争力,影响着医药生物技术进步的方向,所以我国研发队伍的结构和质量仍有待进一步改善。
参考文献:
[1]迈克尔·波特.竞争优势[M].华夏出版社,1997
[2]李心合.技术进步与制度创新:降低企业成本的根本途径[J].中国工业经济, 1996(03)
[3]范光杰,陈光.竞争优势:创新产品选择条件下的波特观点分析[J].科学学与科学技术管理,2004(12)
[4]SharmisthaBagchi-Sen. The Dynamics of Industrial Location: The Factory, the Firm and theProduction System [J]. Economic Geography, 2001, Vol.77, No. 1, p77-79
[5]杨梅英,熊飞,管弦悦,王楠.R&D投入对北京市中小型高新技术企业竞争力的影响[J].科学学研究, 2007(S2)
[6]Jooh Lee and Eunsup Shim. Moderating Effects of R&D onCorporate Growth in U.S. and Japanese Hi-Tech Industries: An Empirical Study[J]. The Journal of High Technology Management Research, 1995(2), volume 6,p179-191
[7]Chambers, D., R. Jennings, and R. Thompson. Excess Returns toR&D-Intensive Firms [J]. Review of Accounting Studies, 2002(7):133-158
[8]程宏伟,张永海,常勇.公司R&D投入与业绩相关性的实证研究[J].科学管理研究,2006(6)
2/2 首页 上一页 1 2 |


