| 本文假定构件组装在一起后不会产生死锁和非法状态等情况,即在设计阶段已验证了所选择构件的可组装性,在组装阶段只考虑如何将构件组装在一起和相应的测试工作。
3 CT-on-IP方法
假定构件都已通过单元测试,通过分析构件匹配的接口操作,可以确定组装后构件之间的交互路径,由此可以在不进行模型组合的情况下生成组装测试用例。
3.1构件运行序列
本节先给出几个相关定义,设 为构件的接口自动机模型。 为构件的接口自动机模型。
定义4 (运行):对于 中的任意执行片段: 中的任意执行片段: ,其中: ,其中: 模型组合, 模型组合, , , ,若 ,若 或 或 则称 则称 为 为 中的运行。为简化说明,本文中只考虑 中的运行。为简化说明,本文中只考虑 的情况。 的情况。
定义5 (简单环):对于P 中的任意执行片段 ,如果 ,如果 满足:(1) 满足:(1) 且 且 ; (2) ; (2)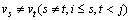 ,则称 ,则称 为简单环,其集合用 为简单环,其集合用 表示。简单环中不包括初始状态且除了头状态与尾状态相同外,不能再有相同的状态出现。 表示。简单环中不包括初始状态且除了头状态与尾状态相同外,不能再有相同的状态出现。
定义6(简单运行): 为 为 的运行,若对于 的运行,若对于 中的任意两个执行片段 中的任意两个执行片段 ,若 ,若 有 有 ,则称 ,则称 为简单运行, 为简单运行, 的简单运行集合用 的简单运行集合用 表示。由定义可知,在一次简单运行中不能出现相同简单环。 表示。由定义可知,在一次简单运行中不能出现相同简单环。
如在图1的构件User中,(a,start?,b,msg!,c,ok?,a)是一次运行也是简单运行,而(b,msg!,c,fail?,b)是一个简单环。与一般意义上的简单回路不同,简单运行中的状态和活动可以重复出现,但环路不能相同。
参照图的深度优先遍历算法,我们给出了简单运行序列的生成算法。首先从初始状态开始查找一个简单运行序列,将此序列作为当前序列 ;从 ;从 中不等于初始状态的最后一个状态开始,寻找可构成与原序列不同的另一个简单运行;若找不到则去掉一个最后状态,继续寻找;若找到,则以新的序列为当前序列,重复上述过程,直到全部简单运行都找到为止。具体算法见附录一。因为在构件行为模型中,活动与状态的数目是有限的,且简单运行要求简单环不能重复出现,所以上述算法一定会结束。 中不等于初始状态的最后一个状态开始,寻找可构成与原序列不同的另一个简单运行;若找不到则去掉一个最后状态,继续寻找;若找到,则以新的序列为当前序列,重复上述过程,直到全部简单运行都找到为止。具体算法见附录一。因为在构件行为模型中,活动与状态的数目是有限的,且简单运行要求简单环不能重复出现,所以上述算法一定会结束。
设接口自动机中变迁的数目为 ,算法1中第一个while循环的时间复杂度为 ,算法1中第一个while循环的时间复杂度为 ;第二个while循环是算法中的主要循环部分,其中确定从 ;第二个while循环是算法中的主要循环部分,其中确定从 发出的所有活动是否都已查找过的复杂度为 发出的所有活动是否都已查找过的复杂度为 ,而在最坏情况下,一个简单运行序列的长度为 ,而在最坏情况下,一个简单运行序列的长度为 ,所以确定是否存在与其构成新的简单运行序列的时间复杂度为 ,所以确定是否存在与其构成新的简单运行序列的时间复杂度为 ,故第二个while循环的时间复杂度为 ,故第二个while循环的时间复杂度为 。综上所述,算法4.1的时间复杂度为 。综上所述,算法4.1的时间复杂度为 。 。
3.2构件组装交互路径分析
通过3.1的分析可知,简单运行序列可以表示出一个构件的运行路径,通过简单运行序列的组合可以确定出构件组装后的交互路径。下面给出简单运行序列组合的概念,为简化说明,在下面的定义中我们只保留简单运行序列中的活动,省略其中的状态信息。
定义7(简单运行序列的可组合性):若构件 和 和 可组合, 可组合, , , , ,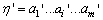 , , ,若满足: ,若满足:
(1) , , , , ; ; , , , ,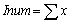 并且 并且 ; ;
(2) , , , ,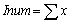 ; ; , , , , 并且 并且 。 。
则称 和 和 可组合中国学术期刊网。条件(1)要求交互接口中由 可组合中国学术期刊网。条件(1)要求交互接口中由 提供给 提供给 的输出都能被接收,条件(2)要求 的输出都能被接收,条件(2)要求 中需要 中需要 提供的输入都能被满足。 提供的输入都能被满足。
定义8 (简单运行序列的组合): , , , , 和 和 可组合,则二者组合的结果 可组合,则二者组合的结果 可按下列方式进行: 可按下列方式进行:
2/4 首页 上一页 1 2 3 4 下一页 尾页 |


