论文导读::本文介绍了DCT域图像水印技术,详细分析了经典的Cox算法和一种基于块分类的自适应图像水印算法;通过分析图像在流通中可能经常遇到的一些信号处理、几何变换以及可能性攻击,对水印算法进行了分析、实验和测试。Cox算法是一种基于DCT变换的扩频水印技术,它将高斯随机序列加入到图像的DCT变换后视觉最重要的系数中。基于块分类的自适应图像水印算法将原始图像分块并设计了一个基于视觉掩蔽特性的分类器,根据分类的结果,不同强度的水印分量被嵌入到不同图像块的DCT低频系数中。实验结果表明,DCT域算法得到的水印图像失真小,对于基本的图像处理操作具有较强的鲁棒性。
论文关键词:数字水印,离散余弦变换,分块,鲁棒性,扩频
1DCT域图像水印
离散余弦变换(discrete cosine transform,DCT)是数字信号处理技术中常用的线性变换技术之一,也是图像压缩中常用的变换编码方法之一。由于任何连续的实对称函数的傅立叶变换中只含有余弦项,所以离散余弦变换与傅立叶变换一样有明确的物理意义。离散余弦变换避免了傅立叶变换中的复数运算,它是基于实数的正交变换,其变换矩阵的基向量很近似于Toeplitz矩阵(系数矩阵对称且沿着与主对角线平行的任一对角线上的元素都相等)的特征向量,而Toeplitz矩阵又体现了人类语言及图像信号相关性特征,故离散余弦变换常被认为是对语音和图像信号的准最佳变换。数字图像可看作二元函数在离散网格点处的采样值,图像的内容通常具有某种程度的自相关性,即图像局部的内容往往变换不大,所以,对数字图像进行离散余弦变换,可以充分利用图像的自相关性减少数据量,达到压缩数字图像的目的。同时,离散余弦变换变换后能量集中,算法复杂度适中,较易于在数字信号处理器中快速实现。
一个长度为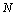 的序列 的序列 的一维离散余弦变换 的一维离散余弦变换 的定义为: 的定义为:
 (1) (1)
 (2) (2)
它的离散余弦反变换(IDCT)由下式表示:
 (3) (3)
在数字图像处理中使用的是二维离散余弦变换,对一幅 图像 图像 ,它的DCT变换为: ,它的DCT变换为:
 (4) (4)
反离散余弦变换(IDCT)为:
 (5) (5)
注:以上格式中

2Cox算法原理
2.1嵌入水印
Cox等人提出的一种基于DCT变换的扩频水印技术[1]扩频,它是一种典型的DCT域算法。该算法将满足正态分布的伪随机序列加入到图像的DCT变换后视觉最重要系数中(其理由是感觉上重要的分量也是对应图像信号的重要分量,携带了大部分的能量,即使图像发生一定的失真,或遭到攻击,仍能保留主要成分),利用了序列扩频技术(SS)和人类视觉特性(HVS)。算法原理为选定视觉最重要系数,再进行修改,采用公式:
 (6) (6)
所示的乘性准则。这里 为嵌入水印序列后的载体图像块; 为嵌入水印序列后的载体图像块; 为原始载体图像块; 为原始载体图像块; 为水印嵌入强度; 为水印嵌入强度; 为待嵌入的水印序列。一般来说,乘性准则的抗失真性能要优于加性准则。 为待嵌入的水印序列。一般来说,乘性准则的抗失真性能要优于加性准则。
2.2 提取水印
基于DCT变换的扩频水印算法的水印提取采用如下公式:
 (7) (7)
确定水印的存在是通过计算。Cox算法水印的检测是通过计算相关函数作相似性运算。从嵌入水印的图像中提取 是嵌入规则的逆过程,把提取出来的水印与原始水印作相似性运算,与指定的阈值比较,可确定是否存在水印。这是稳健性水印的奠基性算法,得到了非常广泛的应用。水印检测是通过比较水印和可能变化的DCT系数间的相关性 是嵌入规则的逆过程,把提取出来的水印与原始水印作相似性运算,与指定的阈值比较,可确定是否存在水印。这是稳健性水印的奠基性算法,得到了非常广泛的应用。水印检测是通过比较水印和可能变化的DCT系数间的相关性 和一个阈值 和一个阈值 而进行的。对待检测的图像 而进行的。对待检测的图像 ,按照与水印嵌入相似的步骤,获得从第 ,按照与水印嵌入相似的步骤,获得从第 至第 至第 个DCT系数 个DCT系数 ,按下式计算 ,按下式计算 和水印 和水印 的相关值: 的相关值:
 (8) (8)
作者在文献中使用的阈值由下式决定:
 (9) (9)
3 一种基于Cox算法的分块DCT算法的实现与分析
许多人在Cox算法的基础上进行了大量的工作,结合基于分块DCT的图像压缩方法,将水印嵌入到受攻击影响最小的系数中,结合人类视觉特性,设计图像的自适应算法。下面探讨一种分块DCT算法[2]。
3.1 水印嵌入与提取算法的步骤
1) 嵌入水印
首先将原始载体图像分成互不重叠块BWblock,每块为 大小,对每块进行DCT变换免费论文下载。为了保证水印的不可见性,选取变换后的DCT系数中纹理较复杂的部分( 大小,对每块进行DCT变换免费论文下载。为了保证水印的不可见性,选取变换后的DCT系数中纹理较复杂的部分( )嵌入水印系数 )嵌入水印系数 ,在纹理较简单的部分( ,在纹理较简单的部分( )嵌入水印系数 )嵌入水印系数 ,本文选择 ,本文选择 。由于视觉上,人眼对纹理越复杂的部分越不敏感,故在纹理较复杂处嵌入幅值较大的水印信息,在纹理较简单处嵌入幅值较小的水印信息。此算法中仍采用公式(6)。 。由于视觉上,人眼对纹理越复杂的部分越不敏感,故在纹理较复杂处嵌入幅值较大的水印信息,在纹理较简单处嵌入幅值较小的水印信息。此算法中仍采用公式(6)。
1/2 1 2 下一页 尾页 |


