| 利用上述均值和近似方差将(5)式右端第二项拆成两项进行考虑

再由切比雪夫不等式,有

可得

即,当 时,(5)式右端第二项收敛于零 时,(5)式右端第二项收敛于零
于是在(5)式令 ,则(5)式变为 ,则(5)式变为
因此,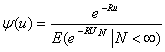 ,得证. ,得证.
推论 2.1  . .
证明:由于 ,所以总是有 ,所以总是有
 ,则 ,则 ,得证. ,得证.
注:在经典模型 中,若理赔额存在上界 中,若理赔额存在上界 ,则有 ,则有 (见文献[5]),但在本文模型中由于有干扰项的存在,即使主索赔和副索赔总额存在上界 (见文献[5]),但在本文模型中由于有干扰项的存在,即使主索赔和副索赔总额存在上界 , , 也不一定成立. 也不一定成立.
参考文献:
[1]Bowers NL. 郑韫瑜译. 风险理论.上海: 上海科学技术出版社,1998.
[2]Dufresne,F.and Gerber, H.U., 1991, Risk theory for the compound Poisson processthat is perturbed by diffusion. Insurance: Mathematics and Economics, 10, 51-/59.
[3]Schmidli,H., 1995, Cramer _/Lundberg approximations for ruin probabilitiesof risk processes perturbed by diffusion. Insurance: Mathematics and Economics,16, 135-149.
[4]王文波,王慧丽,殷春武.一类相依索赔离散风险模型研究.纯粹数学与应用数学,2008,24(2):388-395
[5]熊福生.风险理论.武汉大学出版社,2005.
2/2 首页 上一页 1 2 |


