论文导读::基于含时Ginzburg-Landau(TDGL)方程建立二维超导薄膜经历快速冷却后的拓扑缺陷数目与冷却速度的关系模型。采用差分法对此模型进行了数值模拟,计算出不同冷却速度下拓扑缺陷数目随着时间的变化关系。计算结果发现,在不同冷却速度下,缺陷数目随着时间的变化可以分为两个阶段:第一阶段缺陷数目较多,拓扑缺陷数目随时间急剧减少;在第二阶段,缺陷数目较少,缺陷数目缓慢减少。而且发现,较快的冷却速度有利于形成更多的拓扑缺陷。这种变化趋势与文献[8]报道的实验结果相一致。
论文关键词:超导薄膜,TDGL,KUBB相变,拓扑缺陷,冷却速度
1引言
相变现象一直是凝聚态物理学中的研究热点之一。在文献[1]中,Kibble预言如果一个复序参量系统经历快速冷却后发生相变进入到有序状态,就会产生拓扑缺陷。Zurek[2]发展了Kibble的理论,他预言拓扑缺陷的初始密度是冷却速度的函数。并且KUBB相变,Zurek等人用数值方法研究了一维和二维对称性破缺发生时,拓扑缺陷的数目与冷却速度的关系[3,4]中国期刊全文数据库。以前关于这类现象的研究主要集中在超流体系[5-7]。近期,在实验上二维超导薄膜经历快速冷却后形成拓扑缺陷的现象也有了相关报道[8]。在超导体系中,形成的拓扑缺陷就是磁通量子。但二维超导薄膜经历快速冷缺后形成拓扑缺陷(磁通量子)的数目与冷却速度的关系没有相关的数值模拟。含时Ginzburg-Landau(TDGL)方程是研究超导磁通动力学的一个有力工具[9-15]。基于上述情况,我们基于TDGL方程,采用数值模拟的方法研究了二维超导薄膜在经历快速冷却条件下所形成的拓扑缺陷数目与冷却速度的关系。
数值模拟结果发现,在不同冷却速度下KUBB相变,缺陷数目随着时间的变化情况不同,而且较快的冷却速度有利于形成更多的拓扑缺陷。这种变化趋势与文献[8]所报道的实验结果相一致。
2基于TDGL方程的二维模型
2.1 模型的建立
通过对TDGL方程的矢量和标量势的规范变换,TDGL方程可以进行数值积分并且用于二维超导薄膜经历快速冷却后的拓扑缺陷数目与冷却速度的关系研究中国期刊全文数据库。
本文中对TDGL方程进行的归一化和规范变换如下:
 , , , ,
 , , , , , ,
其中 是一个正的常量KUBB相变, 是一个正的常量KUBB相变, 是热力学临界磁场强度。 是热力学临界磁场强度。 和 和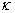 分别定义为 分别定义为 和 和 。 。
经过上述变换后,TDGL方程可以改写为
 (1) (1)
其中波函数Ψ以0K时的平衡值为单位,温度T以超导临界温度Tc为单位,T随时间t的变化关系为 , , 为冷却速度。 为冷却速度。
经过上述变换后,建立的方程即为本文中用于二维超导薄膜经历快速冷却后的拓扑缺陷数目与冷却速度的关系模型。
2.2数值模拟
考虑在X-Y平面上的二维超导薄膜。首先对TDGL方程进行离散化为差分方程。我们取一块单位晶胞 (600ξ×600ξ), (600ξ×600ξ), 和 和 分别表示单位晶胞沿x方向和y方向的长度,包含 分别表示单位晶胞沿x方向和y方向的长度,包含 (2400×2400)个晶格点KUBB相变,在此二维区域上离散TDGL方程,采用差分法中的九点差分格式离散空间变量。 (2400×2400)个晶格点KUBB相变,在此二维区域上离散TDGL方程,采用差分法中的九点差分格式离散空间变量。 和 和 分别表示X方向和y方向的网格间隔,取值0.25。在我们的模拟里,采用欧拉方法求解中国期刊全文数据库。其余相关变量的初值分别为 分别表示X方向和y方向的网格间隔,取值0.25。在我们的模拟里,采用欧拉方法求解中国期刊全文数据库。其余相关变量的初值分别为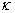 =2, =2, =1, =1,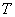 =0.5,设置好初值后就开始进行模拟。 =0.5,设置好初值后就开始进行模拟。
模拟时的边界条件有自然边界条件和周期性边界条件两种。文中采用后者,因为周期性边界条件能够较好的给出拓扑缺陷的动力学行为。根据本文的TDGL模型KUBB相变,采用的周期性边界条件为:
 (2) (2)
在模拟计算过程中,逐渐增加晶格点数目,最后达到了满意结果。接近Tc时计算较长时间, 达到平衡后再降温。
2.3结果与讨论
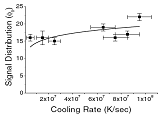
本文得到的模拟结果如图1和图2所示。图1显示了不同冷却速度下,缺陷数目随着时间的变化。曲线可以分为两个阶段,第一阶段缺陷数目较多,间距较小,涡旋方向相反的磁通量子由于近程作用而靠近湮灭,拓扑缺陷数目随时间急剧减少;在第二阶段KUBB相变,缺陷数目较少,间距较大,磁通量子间的相互作用较弱,缺陷数目缓慢减少。在这两个阶段的分界点处缺陷数目与冷却速度的关系见图2,较快的冷却速度有助于形成更多的拓扑缺陷中国期刊全文数据库。
|

|
|
图1.不同冷却速度下缺陷数目随着时间的变化曲线
Fig. 1The number of defects during different cooling rate
|
|
|
|
图2. 第一二阶段分界处缺陷数目与冷却速度的关系。插图为文献[8]中的实验结果
Fig. 2The relation of number of defects and cooling speed at the demarcation point
between the first stage and the second stage. The illustration is the experiments
results in document [8].
|
3 结论
建立了基于TDGL方程的二维超导薄膜在快速冷却条件下的拓扑缺陷数目与冷却速度的关系研究模型,采用差分法对此模型进行数值模拟。计算结果发现,在不同冷却速度下,缺陷数目随着时间的变化可以分为两个阶段:第一阶段缺陷数目较多KUBB相变,拓扑缺陷数目随时间急剧减少;在第二阶段,缺陷数目较少,缺陷数目缓慢减少。而且发现,较快的冷却速度有利于形成更多的拓扑缺陷。这种变化趋势与文献[8]报道的实验结果相一致。
研究二维超导薄膜中拓扑缺陷数目与冷却速度关系是超导磁通动力学领域的一个很重要的问题,它不仅帮助人们理解超导磁通本身的生成与湮灭的本征特性,也为超导薄膜在应用方面的探索提供一定的参考。
[1] Kibble TW B, 1976 Phys .J A 9 1387
[2] W. H. Zurek 1985Nature (London) 317 505; 1996 Phys.Rep. 276 177
[3] Pablo Laguna,Wohciech Hubert Zurek 1998 Phy. Rev. D 58 085021
[4] Andrew Yates,Wojciech H. Zurek 1998 Phys.Rev.Lett. 80 5477
[5] Hendry P C ,Lawson N S, Lee R A M, McClintock P V E, and Williams C H D , 1994Nature(London) 368 315
[6] Ruutu V M H,Eltsov V B, Gill A J, Kibble T W B, Krusius M, Makhlin Y G, Placais B, VolovikG E, and Xu Wen, 1996 Nature(London)382 334
[7] B?uerle C,Bunkov Yu M, Fischer S N, Godfrin H, and Pickett G R, 1996 Nature(London)382332
[8] Maniv A,Polturak E, Koren G 2003 Phys.Rev.Lett. 91 197001
[9] Kato R,EnomotoY and Maekawa S 1993 Phys.Rev. B 47 8016
[10] RyuzoKato,Yoshihisa and Enomoto 1991 Phys.Rev. B 44 6916[11] Du Q, GunzburgerM D and Peterson J S 1995 Phys.Rev. B 51 16194
[12] Tang Q andWang S 1995 Physica D 88139
[13] Du Q 1994 Appl.Anal.52 1
[14] Fram H,UllahS and Dorsey A T 1991 Phys.Rev.Lett. 66 3067
[15] Liu F,Mondello M and Goldenfeld N 1991 Phys.Rev.Lett. 66 3071
Study on the Relation of the Numbers of Topological Defects andCooling Rate During a Rapid Quench in Two-Dimension Superconducting Films
JIN Xiang , WU Hong-Ye , LIUGui-Xiang, ZHAO Jian-Jun , LU Yi , Fan Yong-Sheng
(Departmentof Physics, Baotou Teachers College, Baotou, 014030)
Abstract: A model was build about the relation of the numbers of topological defects and cooling rate duringa rapid quench in two-dimension superconducting films based on Time-Dependent Ginzburg-Landau(TDGL).We present numerical solutions of the modelby a difference approximation, and compute the numbers of topological defectschanging with time during different cooling rates. The results show that thecurve of the numbers of topological defects changing with time during differentcooling rates can be divided into two stages. In the first stage, the numbersof topological defects are more. And the number of topology defects fall offrapidly with time. In the second stage, the numbers of topological defects falloff slowly with time. This was consistent with the experiment results reportedin document [8].
Key words: superconducting films,TDGL,KUBB phasetransition,topological defects,coolingrate
PACC: 7460G,7475
* Project supported by National NaturalScience Foundation of China (Grant Nos.50862007 and 11064008); Research andInnovation Teams of Baotou Teachers’ College.
|


