论文摘要:由一维波动方程得到两组特征线,依次沿着两组特征线推导,可以得出一维非齐次波动方程始值问题的解。这样在教材方法之外,可以完全用特征线方法推导出一维非齐次波动方程始值问题的解。
论文关键词:一维非齐次波动方程,始值问题,特征方程,特征线
对于一维非齐次波动方程
通过文献[1]的叠加原理、 公式及齐次化原理,其解可表示为 公式及齐次化原理,其解可表示为
本文通过完全的特征线方法推出方程(1)的解(2)。将方程(1)的第一式表示为
令 (4) (4)
由(3)有 (5) (5)
由(1)中始值条件,有
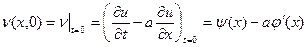
方程(5)的特征方程 确定方程(5)的特征线 确定方程(5)的特征线
其中 0是任意常数, 0是任意常数, 取不同值得到不同的特征线。沿着特征线 取不同值得到不同的特征线。沿着特征线 并由(5)有 并由(5)有
 ,从而 ,从而
 这样,沿着特征线 这样,沿着特征线 有 有
 方程(4)的特征方程 方程(4)的特征方程 确定方程(4)的特征线 确定方程(4)的特征线
其中 是任意常数, 是任意常数, 取不同值得到不同的特征线。沿着特征线 取不同值得到不同的特征线。沿着特征线 并由(4)有 并由(4)有
 ,(7) ,(7)
由(6)和(7)两式可见,沿着特征线
 由始值条件 由始值条件 ,有 ,有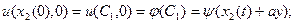 (9) (9)
 交换积分次序,有 交换积分次序,有

取代换 ,则上式等于 ,则上式等于
 0由(8)~(11),可得到 0由(8)~(11),可得到
 将其中的 将其中的 写为 写为 ,即得到(2)。 ,即得到(2)。
参考文献
1 谷超豪,李大潜,陈恕行,郑宋穆,谭永基.数学物理方程.北京:高等教育出版社,2002,6—15. |


