| 在此基础上,可以把原有的4个运算阶段(stage1,stage2,stage3,stage4)合并为2个。
3.2合并简化计算
在进行了权重系数分解后,可以把2个阶段的蝶形运算合并成一个,由此减少了程序运行过程中循环执行次数,也就减少了执行期间从内存读写权重系数和x[]的次数,从而使得算法执行速度获得较大提高。在s(s=1,2……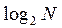 )阶段,共有N/ )阶段,共有N/ 个不同的权重系数,每个系数按如下法则递归生成: 个不同的权重系数,每个系数按如下法则递归生成:
第一个和第二个分别是: , , (k= (k= ) )
第三个和第四个分别是: , ,
第五个和第六个分别是: , ,
……
该法则类似Fibonacci数列
X[n+N/ ] ]
|
|

图2(a)
X[n+N/ ] ]
|
|

图2(b)
图2(a)显示了在s和s+1阶段的蝶形运算规则,其中在图2(b)中被挖掉的节点表示此处由于x[n]带来的内存访问操作被消除。消除的原因是由于原本的2个阶段合并成一个阶段,此处的读x[n]操作只会在一次stage循环中被执行,而不会被执行2次。由4.1章节中三角恒等变换公式可得2 = = ,因此,只需从内存中访问 ,因此,只需从内存中访问 和 和 这2个系数,就可以对图2(a)中的4个蝶形运算进行计算,据此,图2(a)中的2个阶段可以合并成1个阶段,即图2(b)所示。在3.1章节中提到,FCTPruning的蝶形运算部分可分为 这2个系数,就可以对图2(a)中的4个蝶形运算进行计算,据此,图2(a)中的2个阶段可以合并成1个阶段,即图2(b)所示。在3.1章节中提到,FCTPruning的蝶形运算部分可分为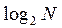 个阶段(stage),改进后对运算阶段进行了合并,使得stage数量减少为: 个阶段(stage),改进后对运算阶段进行了合并,使得stage数量减少为:
  为奇数 为奇数
  为偶数 为偶数
改进后PruningFCT蝶形运算部分设计如图(3)所示:

注:a=[ - - ]/2,b=[ ]/2,b=[ - - ]/2,c=[ ]/2,c=[ - - ]/2 ]/2
e=[ - - ]/2 ]/2
图(3)
4对算法的分析和验证
通过上述的改进设计,由权重系数和x[n]输入引发的内存访问操作进一步减少。以图1和图3中16-pt的FCT为例,图1中显示,16-pt的FCT中共有15个权重系数,经过分解后图3中权重系数降低为10个。图1中由x[n]输入引发的内存访问有128次,即图1中实心圆和空心圆的数量,图3中经过合并,stage数量由4个合并成2个,程序段2算法中最外层对stage的循环次数减少为2次,大量的x[n]重复访问被省掉,由x[n]输入引发的内存访问由是减少为64次,即图3中实心圆和空心圆的数量。对于PruningFCT算法,输入序列数量N=16,当 =3时,图1中由x[n]输入引发的内存访问有87次,图3中由x[n]输入引发的内存访问有43次。 =3时,图1中由x[n]输入引发的内存访问有87次,图3中由x[n]输入引发的内存访问有43次。
通过简单对比显然易见,改进后的PruningFCT算法内存访问次数进一步降低,这必然提高运行速度。为了更好的显示改进的效果,将文中程序段1和程序段2针对同样的输入序列在C64XDSP平台上运行,输入序列分别为8-pt,16-pt,32-pt,64-pt的一维数组。输出 为了方便起见,只取2的整数次幂,实验结果如下表: 为了方便起见,只取2的整数次幂,实验结果如下表:
|
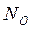
N
|
2
|
4
|
8
|
16
|
32
|
64
|
|
8
|
程序段1
|
41
|
54
|
70
|
|
|
|
|
程序段2
|
23
|
36
|
52
|
|
16
|
程序段1
|
89
|
118
|
150
|
194
|
|
程序段2
|
42
|
65
|
81
|
125
|
|
32
|
程序段1
|
185
|
246
|
310
|
386
|
498
|
|
程序段2
|
95
|
140
|
172
|
248
|
360
|
|
64
|
程序段1
|
377
|
502
|
630
|
770
|
945
|
1218
|
|
程序段2
|
188
|
273
|
321
|
429
|
541
|
813
|
表1
PruningFCT算法改进前改进后对内存的占用情况如下表:
|
N
|
8
|
16
|
32
|
64
|
|
程序段1
|
14
|
30
|
62
|
126
|
|
程序段2
|
10
|
20
|
41
|
84
|
表2
由表1和表2中试验数据可见,改进后的算法无论在内存访问时间上还是内存占用方面都有了明显提升,对表1的数据进行计算分析得出,平均访问次数降低了41.5%;对表2的数据分析表明,内存占用减少了32.2%。
5总结及后续发展
本文介绍了一种对PruningFCT算法改进设计,该设计的基本思想是利用三角恒等变换,把s+1阶段的权重系数用s阶段的权重系数来替代,从而减少了算法中的权重系数,进而把蝶形运算中的阶段合并,减少了阶段数量,从而减少了对输入序列的访问次数。试验结果显示,改进后的算法不仅降低了内存访问次数,还减少了内存的占用。文中只对一维的PruningFCT算法进行了改进,二维的PruningFCT算法在图像压缩中的应用更有实际意义,下一步可沿用文中所提思想对二维的PruningFCT算法进行改进。
参考文献
1 N. AHMED, T. NATARAJAN, and K. R. RAO “DiscreteCosine Transform,” IEEE Transactions on Computers, vol. C-23, pp.90-93, January 1974.
2 K. R. Rao and P. Yip, Discrete Cosine Transform: Algorithms,Advantages, Applications. New York: Academic, 1990.
3 M. Wezelenburg, “General radix-2n DCT and DST algorithms,”Proceedings of the International Conference on ECCTD’97,pp.789-794, Budapest, Hungary, September 1997.
4 Y.-H. Chan and W.-C. Siu, “Mixed-radix discrete cosinetransform,” IEEE transactions on Signal Processing, vol. 41,no.11, pp. 3157-3161, November 1993.
5 Z. Wang, “Pruning the fast discrete cosine transform,” IEEETrans. Commun. vol. 39, no. 5, pp. 640-643, May 1991.
6 Athanassios N. Skodras, “Fast Discrete Cosine TransformPruning,” IEEE Trans. On Signal Processing, Vol. 42, no. 7,pp.1833-1837, July 1994.
7 S.C.Chan and K.L.Ho “A new two-dimensional fast cosinetransform algorithm,” IEEE Trans. Signal Processing,vol. 39,no. 2, pp. 481-485, February 1991. 2/2 首页 上一页 1 2 |


