论文导读::实证检验与估计。政府支出的经济增长效应分析—基于内生结构突变模型。
论文关键词:政府支出结构突变,增长效应,实证检验
一、引言
政府支出的效应问题一直是经济学界关注的热点话题之一且存在很大争议。活跃于50年代末60年代初,以Solow为代表的新古典增长理论认为,政府支出只具有短期效应而无长期的经济增长效应。80年代末90年代初,以Lucas和Romer为代表的新生增长理论认为,由于知识、基础设施等具有外部性,政府须干预经济,政府对私人投资的补充对经济具有正向作用但尚未建立一致定论的内生增长模型。Barro(1990)将政府支出引入到内生增长模型,从政府生产性支出和消费支出的角度进行研究,得出政府支出具有生产性。Alfred Greiner(1996)认为在一定的条件下,线形生产技术、外溢效应、生产性公共资本、人力资本投资和开发对经济增长都有正效应。
经验研究方面关于政府支出对经济增长的影响则是混合的。Grier和Tullock (1987)对115个国家30年的数据进行分析,得出政府消费支出占实际GDP之比与实际GDP正相关;Aschaur (1989)考察美国1949-1985年的生产率和公(私)资本之比,发现两者为正关系;Landau(1983)对115国的数据分析本科毕业论文格式,发现人均GDP与政府消费支出占GDP之比率负相关;Barro(1991)对98个国家1960-1985年的政府消费支出与人均GDP进行研究,得出政府消费对增长有显著负作用的结论;Easterly Rebelo(1993)对28个国家1970-1988年间的公共投资与经济增长进行实证分析,两者正关系。在这些文献中,由于方法的差异、样本数据等不同必造成混合的结论。显然,这就需要采用更稳健的研究方法,以期得到可靠的结果。近年来,国内一些学者在实证方面作了大量的研究,主要沿着两条思路展开:一是按照Barro的研究路线把政府支出分为生产性支出和非生产性支出,然后在C-D模型的基础上进行分析;二是从总量上考察政府支出与经济增长的关系。
综观已有的经验研究成果,这方面的工作主要有横截面数据回归和时间序列分析等两方面:一方面,在计量方法并不成熟的条件下,人们普遍采用横截面数据进行回归分析;另一方面,随着研究方法的日趋完善,时间序列方法已成为目前这方面研究的主流分析工具。但以上研究方法存在一定的局限,如没考虑时间序列的非平稳性,研究的结果有可能建立在伪回归的基础上;最常用的做法是采用误差修正及向量自回归模型,由于未考虑时间序列变量是否存在结构突变可能降低检验势,其结论也缺乏普遍性和准确性。
由于体制的变化,使得样本的DGP可能存在结构突变的问题。从计量经济学的角度看,如果忽视这种现象进行一般的单位根与协整分析,结果将出现很大的偏差。为此,本文利用Eviews6.0和Gauss8.0对建国以来的政府支出和GDP进行突变检验,考虑数据的依赖特征以及制度改革冲击对经济增长的影响,尝试性地解释造成这种现象的原因。本文的结构安排如下:第二部分是相关的模型和经济原理框架;第三部分是实证检验;最后是结论及存在的问题杂志铺。
二、突变模型框架
在现有计量检验的文献中,一般都假定不存在结构突变。如果忽视这种结构变化,则传统的单位根检验拒绝原假设的势就会下降。Perron (1989)在ADF检验基础建立相对完备的理论体系,成为突变问题研究的里程碑[③]。尽管国内存在一些单结构突变检验的文献,但基本上都是采用外生突变检验,存在很强的主观性。ZA检验和LP检验可以避免这一问题,而检验假设却存在一定的问题[④]。为此,本文在内生单突变检验上采用perron的模型,而对于内生双突变则借鉴Junsoo lee and MarkC.Strazicih的最小LM单位根检验模型和方法。
(一)内生单突变模型
Perron(1989)针对突变点已知给出三种经验模型:截距突变的“崩溃”模型A、斜率突变的“增长变化”模型B、截距和斜率突变的“混合”模型C[⑤]。原假设是带结构突变的单位根过程,而备选是带结构突变的趋势平稳过程,为简单起见说,只给出最具有一般性的模型C[⑥]。原假设单和备选假设所分别对应的方程为:
 : : (1) (1)
 : : (2) (2)
其中 (3)。 (3)。 代表突变点本科毕业论文格式, 代表突变点本科毕业论文格式, =1,当t=Tb+1时; =1,当t=Tb+1时; =1,当 =1,当 时;其他情况下为0。在模型的选择上,通过比较各种模型在检验势和结构框架的一致性,采用从一般到特殊的检验,如先检验模型C,然后使用更多的约束条件来评估检验结果的稳健性。在对退化趋势进行检验时,需要对“附加异常值”(additive outlier AO)模型和“新息异常值”(innovationaloutlinerIO)模型做出选择[⑦],前者意味趋势函数的变动是瞬时完成而现实的冲击变动是持续很长时间,而后者暗示变动是逐步完成的[⑧]。 时;其他情况下为0。在模型的选择上,通过比较各种模型在检验势和结构框架的一致性,采用从一般到特殊的检验,如先检验模型C,然后使用更多的约束条件来评估检验结果的稳健性。在对退化趋势进行检验时,需要对“附加异常值”(additive outlier AO)模型和“新息异常值”(innovationaloutlinerIO)模型做出选择[⑦],前者意味趋势函数的变动是瞬时完成而现实的冲击变动是持续很长时间,而后者暗示变动是逐步完成的[⑧]。
(二)双结构突变检验
对于双结构突变点检验用Junsoo lee andMark C.Strazicih(2003)提出的minimumLagrange Multiplier unit root test(LM检验),而LP双结构突变检验由于备选假设存在不明确的假定或序列是带突变的差分平稳过程,LP检验在解释中易得到错误的结论。
考虑序列,DGP如下所示[⑨]: , , (4) (4)
这里 是一个外生向量矩阵, 是一个外生向量矩阵, 。双突变的LM单位根检验的统计量可以按照如下的LM(得分)原则回归得到: 。双突变的LM单位根检验的统计量可以按照如下的LM(得分)原则回归得到: (5) (5)
这里 ,(6) ,(6)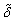 是回归系数; 是回归系数; 由 由 得出。单位根的原假设是 得出。单位根的原假设是 =0,L:M统计量由下式得到: =0,L:M统计量由下式得到: (7) (7) 为原假设 为原假设 时的检验统计量。 时的检验统计量。
双突变的LM单位根检验通过格点搜索来确定突变的时点,利用最小的检验统计量对应的 值来确定突变点。用计算机软件编程可直接求得突变时点和个数,本文在Lee(2004)Gauss双突变LM单位根检验程序代码基础上修改运行程序获得突变时点和个数。通过比较Lee和Strazicich计算的内生双突变统计量,判断是否存在突变点。 值来确定突变点。用计算机软件编程可直接求得突变时点和个数,本文在Lee(2004)Gauss双突变LM单位根检验程序代码基础上修改运行程序获得突变时点和个数。通过比较Lee和Strazicich计算的内生双突变统计量,判断是否存在突变点。
1/2 1 2 下一页 尾页 |


